Das
trinitarische Prinzip 1 und 3
I. Das Flächenverhältnis der beiden
Tetraktyskreise
II. Verhältnisse
der Tetraktysseite
III. Die
Zahlen 14 und 17
VI. Die trinitarischen
Verhältnisse in der Kapitolinischen Trias
VII. Die Zahlen 6 und 11
VIII. MARIA
IESUS
IX. 3 und 4 als Kreis- und Wiederkehrprinzip des Dezimalsystems
im Namen BARBARA
I. Das Flächenverhältnis der beiden
Tetraktyskreise
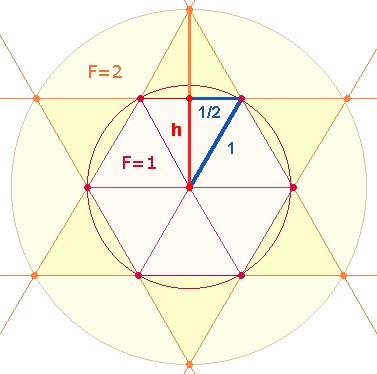
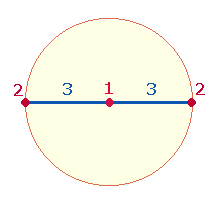
1. Der
Tetraktysstern (das Hexagramm) mit seinen zwei konzentrischen Kreisen ist ein
wesentliches Modell des Dezimalsystems, das in sich Einheit und Dreiheit darstellt und damit den einen Gott in drei Personen abbildet. Dieses
Modell ist in sich geschlossen, während ein rechtwinkliges Achsenkreuz als
Ausgangspunkt sich in endloser quadratischer
oder kreisförmiger Ausdehnung entfalten kann.
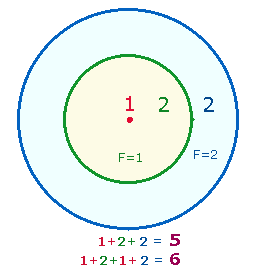
Die Einheit in der Dreiheit
verwirklicht sich geometrisch, indem eine erweiterte Figur aus drei Einheiten konzentrisch ihre
Ausgangsfigur aus einer Einheit überlagert. Es handelt sich dabei erstens um zwei konzentrische
Kreise, zweitens um die Tetraktys, deren drei Seiten aus jeweils drei Maßeinheiten bestehen, von
denen die mittlere eine Segmentlinie des hexagonalen Kreises darstellt:
|
|
Die Fläche des äußeren Kreises
beträgt das Dreifache des inneren. Der Beweis ist nach dem Satz des Pythagoras
zu führen, der besagt, daß in einem
rechtwinkligen Dreieck die Flächeninhalte der Kathetenquadrate gleich dem
Flächeninhalt des Hypothenusenquadrats sind.
Der Radius des äußeren
Kreises ist zweimal die Höhe (2h) eines gleichseitigen Dreiecks mit dem angenommenen Längenmaß 1:
h² = 1-(1/2)²;
h² = (4-1)/4; h² = ¾
h = √¾; h = 1/2√3; 2h = √3
Die Fläche eines Dreiecks
ist Grundlinie
mal Höhe durch 2,
Grundlinie ist 1,
Höhe 1/2√3, die Fläche 1/4√3. √3 = 1,7320… Die Fläche eines gleichseitigen
Dreiecks ist demnach – ohne Berücksichtigung des Komma – 1732/4 = 433.
Das Verhältnis der beiden
Kreise ist
1²p : (√3)²p = 1:3
2. Dem
Flächenverhältnis 3:1 der beiden konzentrischen Kreisfiguren zum Hexagon entsprechen 13:7 Punkte, die den 13,7 Milliarden Jahren des
Weltalls eine Erklärungsmöglichkeit geben.
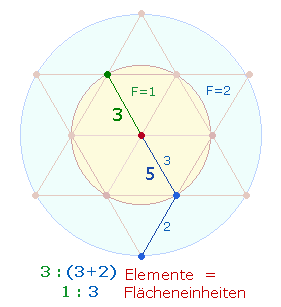
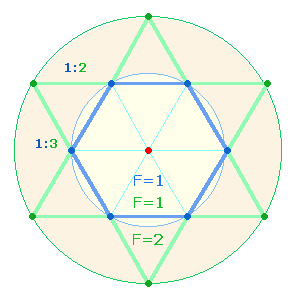
3. Es sind zwei
Flächenverhältnisse zu berücksichtigen: die Fläche des Hexagons zum erweiterten
Kreisring beträgt 1:2 und zum ganzen äußeren
Kreis 1:3. Die Zahlen der beiden
Flächenverhältnisse seien verkürzt die
trinitarische Zahlen genannt. Sie besitzen Relevanz als zweistellige oder vierstellige
Zahlen mit Umkehrungen in Additionen und Multiplikationen, z.B. 12+13 = 25;
12+31 = 43; 21*31 = 651; 2113.
Die entsprechenden Komplementärzahlen der
Grundzahlen 1-9 zu den trinitarischen Kreisflächengrößen 1+3 und 1+2 sind 9+7 = 16 und 9+8 = 17. Die FW der
beiden Zahlenpaare sind 6+7 = 13 und 6+6 =
12. Die FW 13 und 12 wiederholen also in in zweistelliger Zusammensetzung die
trinitarischen Kreisflächenverhältnisse. Die Additionen 16+13 und 17+12 ergeben
beide Male 29 und zusammen 58.
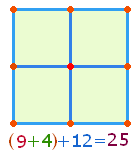
4. Das
Dezimalsystem ist so beschaffen, daß Einzelziffern und zusammengesetzte Zahlen in
engem Sinnzusammenhang stehen. Daher ist die Summe 13+12 = 25 von besonderer Bedeutung. Aus 25 Elementen bestehen die
Figuren des zweiachsigen 3*3 Punkte Quadrats und des Hexagon:
|
|
|
Das Hexagon besteht aus 7 Punkten + 6 Dreiecken und 12 Linien. Die Zahl der Linien
ist in beiden Figuren gleich.
Die Zahl der Linien und
Quadrate des 3x3 Punkte Quadrats bilden wiederum eine Quadratzahl,
sodaß sich die Gleichung 3²+4² = 5² ergibt. Die Zahl 25 kann zum Ausgangspunkt des 5x5
Punkte Quadrats genommen werden. Dabei quadriert sich die Zahl der
Einzelquadrate von 4 auf 16.
Die Reihe kann durch weitere Quadrierungen fortgesetzt werden. Die Zahl der Linien ist stets um einen Zähler
geringer als die Zahl der Punkte + Einzelquadrate.
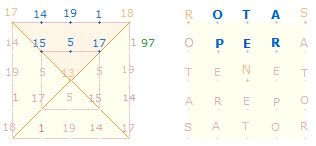
Numeriert man ein 5x5 Quadrat, sind 13 Zahlen ungerade und 12 gerade. Das SATOR-Quadrat ist
ein 5x5 Quadrat, dem ein 3x3 Quadrat zugrunde
liegt. Die Zahlensumme (ZS) und Faktorensumme
(FS) der beiden konzentrischen Quadrate betragen (97+303)
+ (83+249) = 400+332
= 732 = 12*61. Das FS-Verhältnis beträgt 83*(1:3). Das FS:ZS-Verhältnis ist 4*(83:100). Die beiden Verhältniszahlen sind zusammengesetzt
aus den Summen der Zahlen 1-7 + 1-10 und 1-9 + 1-10: 28+55 = 83; 45+55
= 100.
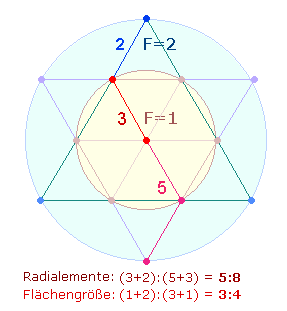
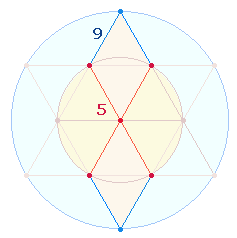
5. Die 5 Durchmesserelemente des Kreises
begründen eine konzentrisch-komplementäre Zahleneinheit, d.h., den
trinitarischen Zahlen 1 und 3 entsprechen
komplementär 5
und 3 (mit Umkehrungen). Ein
geometrisches Modell hierfür sind 3 Radialelemente des inneren Kreises und 5 Radialelemente des
Doppelkreises:
|
|
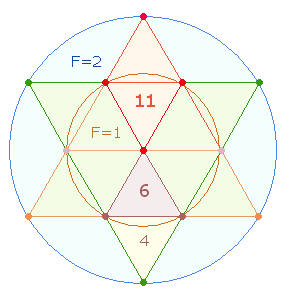
1. Ein Kreis
besteht aus 3 Elementen: dem Mittelpunkt, dem Kreisbogen und der Kreisfläche. Den
beiden trinitarischen Flächenverhältnissen entsprechen daher 5+6 = 11 Kreiselemente:
|
|
Die trinitarischen Zahlen
erscheinen in den Faktorenwerten (FW), wenn man die Elemente des
Kreises (E)
und die entsprechenden Flächeneinheiten (F) zu zweistelligen Zahlen und deren Umkehrungen
zusammensetzt :
|
|
|
|
|
FW |
|
FW |
|
E |
5 |
6 |
56 |
13 |
34 |
19 |
|
F |
3 |
4 |
65 |
18 |
43 |
43 |
|
|
|
|
|
31 |
|
62 |
|
31:62 = 31*(1:2)
= 31*3 |
||||||
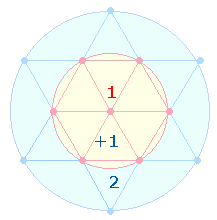
Die Doppelraute spiegelt die
trinitarischen Zahlen spiegelsymmetrisch in 3+1+3 Punkten wider:
|
|
Auch die FW der Umkehrzahlen 122 und 221, dreistellige Zusammensetzungen
der Elemente der beiden Tetraktyskreise, haben dasselbe Ergebnis: 63+30 = 93 =
3*(21+10) = 3*31.
II. Verhältnisse der Tetraktysseite
|
|
1. Die Erweiterung des Hexagons zum
Sechseckstern fügt jeder Maßeinheit eines Segments zwei weitere Maßeinheiten hinzu. Dieser
Erweiterungsvorgang von 1:2 Maßeinheiten stellt gleichzeitig das
Flächenverhältnis der beiden konzentrischen Kreise dar. Insofern aber Hexagon
und Tetraktys zwei eigenständige geometrische Figuren sind, wird jede einzelne
der 6 Segmentlinien überlagert von drei Maßeinheiten, wodurch sich ein Verhältnis 1:3 ergibt. Die beiden Verhältnisse geben gleichzeitig
die Flächengrößen der beiden konzentrischen Kreise wieder, da sich die
Maßeinheiten jeweils in deren Bereich befinden. Die Addition beider
Verhältnisse ergibt entweder 2:5 oder 3:4.
Auf die Punkte allein bezogen,
lauten die Verhältnisse 2:2 + 2:4, zusammen 4:6/4:6. Ihnen entsprechen wiederum die
Flächenverhältnisse 2:5/3:4.
2. Faßt man Segmentlinie + 2 Begrenzungspunkte zusammen, sind die Verhältnisse 3:4 und 3:7 als 1:2 und 1:3 Flächeneinheiten, zusammen 6:11 bzw. 7:10. Der Zahl von 17 Elementen entsprechen 7 Flächeneinheiten.
Man kann die Verhältnisse
auch von den Erweiterungselementen her formulieren: 4:3 und 4:7, zusammen 8:10 bzw. 7:11. Die entsprechenden Flächenverhältnisse sind 2:1 und 2:3, zusammen 4:4 bzw. 3:5.
Es entsprechen somit 17+18 Elementen (Punkte und
Linien) 7+8 Flächeneinheiten. Die
beiden Verhältnisse Punkte zu Linien sind 10:7
und 10:8, zusammen 20:15.
3.
Die
Aufteilungen der Tetraktysseite in 3:4 und 3:7
sind in zweistelliger Zusammensetzung der
ZS 34 und 37 in jeweils drei Buchstaben der äußeren und inneren
Quadratseiten des SATOR-Quadrats vertreten:
|
|
1.
Im Zusammenhang mit der ORANDUM-Formel zeigte sich, daß die Zahlen 14 und 17, Zahlenwerte der Buchstaben
OR, eine besondere Bedeutung
für das SATOR-Quadrat haben. Es scheint, daß diese zwei Zahlen die eben
behandelten beide Aspekte von Flächenverhältnis und Tetraktysseitenverhältnis
zusammenfassen:
Die Zahl 17 ist zu verstehen als 7 hexagonale
und 10
Tetraktyspunkte
Punkte, 14
als die FW
7+7.
1. Aus dem Multiplikationsergebnis
13*23 = 299 läßt sich die Bedeutung mit größerer
Sicherheit feststellen: Numeriert man die Zickzacklinie der Doppelraute vom Mittelpunkt aus von 1-5, ist die Summe 29. Die Durchmesserlinie besteht aus 9 Elementen.
2.
Die beiden Kreisflächenverhältnissen 1:2
und 1:3
können in Relation zur Zahl der
Radialelemente und der Durchmesserelementen gesetzt werden:
|
|
|
3:2 Radialelementen bzw. 5:4 Durchmesserelementen entspricht das
Flächenverhältnis 1:2,
3:5 Radialelementen bzw. 5:9 Durchmesserelementen das Flächenverhältnis 1:3. Die Additionen ergeben 5+8 = 13 und 14+9 = 23. Verdoppelt man
die Radialelemente zu 26, ergibt sich ein Verhältnis von 26+23 = 49 Elementen zu 14+7 = 21 Flächeneinheiten = 7*(7:3). Dem
Verhältnis 7*(7:3)
wiederum, auf 7 hexagonale und 10
Tetraktyspunkte bezogen, entspricht das Flächenverhältnis 1:3.
3.
Aus 2*18
= 36 Elementen bestehen zwei Tetraktysrahmen. Daher ist auch an die
Kreisflächenverhältnisse 1:3 und 2:3 zu denken, denen 3:7 bzw. 4:7 Elemente
einer Tetraktysseite entsprechen, wie oben schon dargelegt wurde.
Wenn man die 3 Eckpunkte der Tetraktys zum
Mittelpunkt in Beziehung setzt, kann man dies als Flächenverhältnis des äußeren
Kreisrings zum inneren Kreis ansehen. 3:1 Punkte bedeuten dann 2:1 Flächeneinheiten. Die einzelne Flächeneinheit 1 des Hexagons wird
repräsentiert durch dessen 6 Kreislinienpunkte mit oder ohne Mittelpunkt. In der numerierten
Tetraktys erhält man so das Summenverhältnis 23:32 oder 23:37:
|
|
VI. Die trinitarischen Verhältnisse in der Kapitolinischen
Trias
1. Die Faktorensummen (FS) der Kapitolinischen Trias enthalten Grundbedeutungen des Tetraktyssterns und als Endziel die Oktaederbildung:
|
IVPPITER |
78 |
|
|
IVNO |
37 |
|
OPTIMVS |
66 |
|
|
REGINA |
49 |
|
|
|
MAXIMVS |
|
MINERVA |
77 |
|
|
144 |
|
48 |
|
144 |
|
144:48:144 = 48*(3:1:3) |
|||||
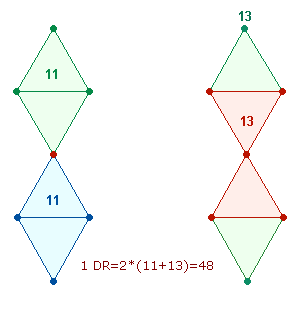
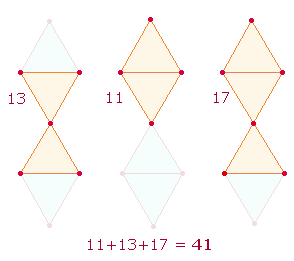
Das Verhältnis 3:1:3 richtet zunächst den Blick auf die Punktestruktur der Doppelraute (DR):
|
|
Der DR liegt ein (sanduhrförmiges) Doppeldreieck zugrunde, das bei der Vereinigung der Endpunkte der DR ebenfalls verdoppelt wird. Das Doppeldreieck besteht aus 13, die Rautenfigur aus 11 Elementen. Bei der Vereinigung zweier Doppelrauten zum Oktaeder kann man eine Umlaufbahn der einen Figur und die zweite der anderen Figur zuordnen. Auf diese Weise erhält man 2*(26+22) = 48:
|
|
Bemerkenswert sind 22+26 als ZS
der Initialen IN-RI und der Buchstabenzahlen der historischen und der biblischen
Kreuzesinschrift.
2. Das Verhältnis 3:1:3 nimmt jedoch auch Bezug zu den eingangs behandelten Flächenverhältnissen. Die FS der weiblichen Bezeichnungen haben keinen gemeinsamen Teilungsfaktor. Sie sind in ihrer Gesamtheit durch 48 teilbar. Der Faktor 3 bezieht sich daher auf die gesamte Flächengröße 3 des äußeren Kreises.
Die FS 48 von MAXIMUS steht für die Flächengröße 1 des hexagonalen Kreises. Die zwei Namen IUPPITER OPTIMUS repräsentieren die Flächengröße 2 des vom hexagonalen Kreis ausgesparten äußeren Kreisrings:
|
|
Da die FS 144 jedoch 48 dreimal enthält, ist auch die durch den hexagonalen Kreis verdeckte Fläche hinzuzurechnen. Diese Deutung wird gestützt durch das Verhältnis 78:66 = 6*(13:11). Die Zahl 13, bezogen auf das hexagonale Doppeldreieck repräsentiert die Flächengröße 1, die bei der Erweiterung gebildete Raute die Flächeneinheit 2 des Kreisrings.
1. Die Verhältnisse 1:3 und 1:2, die für die beiden konzentrischen Kreise des Tetraktyssterns festgestellt wurden, treffen in gleicher Weise für die ZS+FS der Zahlen 1-6 und 1-11 zu:
|
|
|
|
|
|
|
|
sm |
|
|
|
|
|
sm |
GS |
|
ZW |
1 |
2 |
3 |
4 |
5 |
6 |
21 |
7 |
8 |
9 |
10 |
11 |
45 |
66 |
|
FW |
1 |
2 |
3 |
4 |
5 |
5 |
20 |
7 |
6 |
6 |
7 |
11 |
37 |
57 |
|
|
|
|
|
|
|
|
41 |
|
|
|
|
|
82 |
123 |
Es scheint zwei geometrische Bezugspunkte zu geben:
·
Die numerierte Kreisachse:
|
|
Die Numerierungssumme 6:11 entspricht dem Verhältnis von 3 Radialelementen zu 5 Durchmesserelementen, das somit als Vorstufe der 3:5 Radialelemente der beiden konzentrischen Kreise angesehen werden kann.
·
Die Raute und die
"Fischfigur" in der Tetraktys und der Doppelraute:
|
|
Die Zahlen 1-11 sind hier rückwärts 11-1 zu lesen. Die Bewegung der Konstruktion des Hexagramms vom Mittelpunkt nach außen wird hier von außen zur Mitte zurückgeführt. Die Raute aus 11 Elementen nimmt ihren Anfang in einem Punkt des äußeren Kreisbogens und endet im Mittelpunkt und vertritt somit 3 Kreisflächeneinheiten. Es bleibt ein Rest von 6 Elementen, die dem hexagonalen Kreis angehören und somit 1 Flächeneinheit repräsentiert.
11:6 Elemente bedeuten also 3:1 Flächeneinheiten, das ZS+FS-Verhältnis 41*(3:1) und 2:1 Dreiecke. Die Zahl 41 bezieht sich besonders auf die drei Figuren, die in einer Tetraktys und einer Doppelraute zu erkennen sind:
|
|
|
|
1. Wie alles Gute, das menschliche Kultur hervorgebracht hat, ist auch römische Gematrie Ergebnis göttlichen und menschlichen Zusammenwirkens. Welche zentrale Bedeutung den beiden Kreisflächenverhältnissen 1:2 und 1:3 zukommt, zeigt sich an den vierstelligen 4Werte-Summen von MARIA und IESUS, wobei die römischen Zahlzeichen MI und IV mit einbezogen werden. Es ergeben sich so 2*8 Einzelwerte:
|
|
ZS |
FS |
sm |
FW1 |
FW2 |
sm |
GS |
|
MARIA |
40 |
32 |
72 |
11 |
10 |
21 |
93 |
|
MI |
1001 |
22 |
1023 |
31 |
13 |
44 |
1067 |
|
sm |
1041 |
54 |
1095 |
42 |
23 |
65 |
1160 |
|
IESVS |
70 |
36 |
106 |
14 |
10 |
24 |
130 |
|
IV |
6 |
6 |
12 |
5 |
5 |
10 |
22 |
|
sm |
76 |
42 |
118 |
19 |
15 |
34 |
152 |
|
GS |
1117 |
96 |
1213 |
61 |
38 |
99 |
1312 |
|
93 = 3*31; 130 = 10*13; 1312 =
32*41 >51 |
|||||||
|
1035:54
= 9*(115:6) = 9*11²; 1067:22 = 11*(97:2) |
|||||||
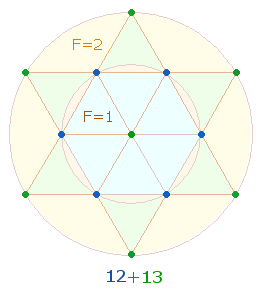
2.
Die beiden Kreisflächenverhältnisse 1:3
und 1:2
werden durch 12+13 und 13+12
Elemente des Tetraktyssterns folgendermaßen wiedergegeben:
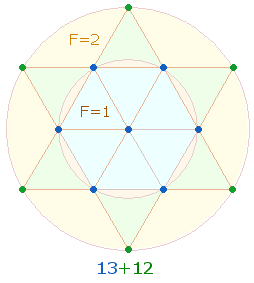
·
1:3 durch 6
Keislinienpunkte + 6 Dreiecke des hexagonalen
Bereichs und Mittelpunkt + 6 Punkte + 6
Dreiecke des Erweiterungsbereichs;
|
|
·
1:2 durch Mittelpunkt + 6 Punkte + 6 Dreiecke des hexagonalen Bereichs und 6 Punkte +
6 Dreiecke des Erweiterungsbereichs.
3.
Wenn man die ZW von IESUS und MARIA
jeweils aufaddiert, bis eine Gipfelsumme zustande kommt, erhält man als
Ergebnis das Verhältnis 37:34, das unter II.3 besprochen wurde:
|
|
|
|
|
888 |
|
|
|
|
|
816 |
|
|
|
|
263 |
625 |
|
|
|
|
254 |
562 |
|
|
|
78 |
185 |
362 |
|
|
|
80 |
174 |
308 |
|
|
23 |
55 |
107 |
177 |
|
|
25 |
55 |
94 |
134 |
|
9 |
14 |
32 |
52 |
70 |
|
12 |
13 |
30 |
39 |
40 |
|
9 |
5 |
18 |
20 |
18 |
|
12 |
1 |
17 |
9 |
1 |
|
I |
E |
S |
U |
S |
|
M |
A |
R |
I |
A |
|
888:816 = 24*(37:34)
= 1704 |
||||||||||
Erstellt: Januar 2011
Zuletzt
bearbeitet: April 2022