DAS SATOR/ROTAS-QUADRAT
STRUKTURELLE
GESICHTSPUNKTE (2)
II. Konstruktion eines 5*5 Punkte-Quadrats
III. Vergleich des Quadrats mit dem
Tetraktysstern
II.
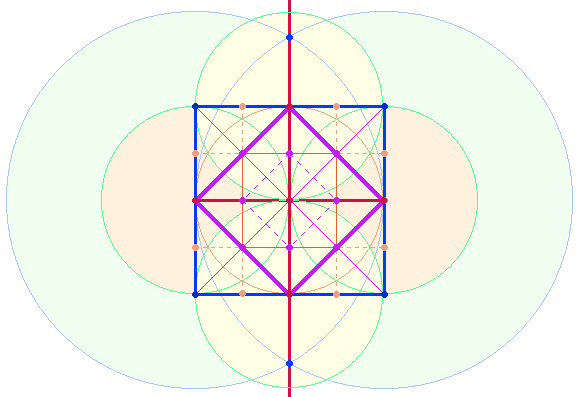
Konstruktion mit Zirkel und Lineal
|
|
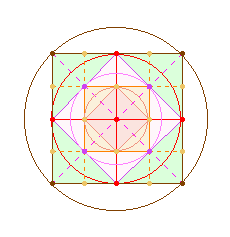
1. Die
Konstruktion beginnt mit einem Kreis und einer horizontalen Mittelachse. Um die
beiden Kreislinienpunkte schlägt man zwei Kreise mit
doppeltem Radius und zieht eine senkrechte Gerade durch beide Schnittpunkte.
Nun liegen die Kreislinienpunkte für die Vertikalachse fest. Verbindungslinien zwischen den 4 Kreislinienpunkten lassen ein Rautenquadrat entstehen.
Um die 4 Eckpunkte des Rautenquadrats schlägt man
sodann je einen Kreis, um 4 weitere Schnittpunkte für die
4 Außenpunkte des Quadrats zu erhalten. Nach dem
Einzeichnen der äußeren Quadratlinien zieht man zwei Diagonalen, die das
Rautenquadrat 4-mal schneiden. Von den 4 Schnittpunkten des
Rautenquadrats aus lassen sich zwei vertikale und zwei horizontale Parallelen zum äußeren Quadratrahmen eintragen, wodurch man
12 weitere Punkte erhält (im SATOR-Quadrat je viermal von
den Vokalen AOE besetzt). Konzentrisch zum äußeren
Quadrat ist nun ein 9-Punkte Quadrat zu erkennen.
Verbindet man die mittleren Punkte der 4 Seiten
dieses inneren Quadrates, erhält man ein weiteres (kleines) Rautenquadrat.
Durch den Einzug der 4 Parallellinien wird die Strecke des Radius halbiert. Wenn man die
Halbierung auf den Wert 1 heraufsetzt, besteht nach Fertigstellung der Figur der
Radius des Ausgangskreises aus zwei Einheiten. Schlägt man um das äußere und innere Quadrat und um das
kleine Rautenquadrat jeweils einen Kreis, ist das Verhältnis der 4 Kreise 1:2:4:8. Die Flächengröße der 4 Quadrate schreitet in Zweierpotenz fort: 2+4+8+16=30. Vom kleinsten Quadrat beginnend, führt die Punktezahl der
ersten drei Quadrate 5+9+13 = 27 durch
Hinzufügung der Gesamtzahl 25 zum Umkehrwert 52.
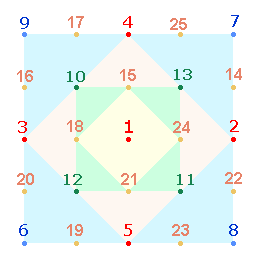
2. Entsprechend den 4 Konstruktionsschritten kann man die 25 Punkte der
Reihe nach so numerieren, daß einerseits die Fortsetzungsrichtung nach rechts, andererseits
der jeweilige Gegenpol gesucht wird. Die Zahlen 14-25 folgen den eingezogenen
Parallelen (jeweils 3 vor einer Richtungsänderung). Die rechte Grafik zeigt die
ZW des SATOR-Quadrats:
|
|
|
Der 1. und 4. Konstruktionsschritt mit 5+12 = 17 Punkten verläuft horizontal und vertikal, der 2. und 3. mit 4+4 = 8 Punkten diagonal. Es ist denkbar, daß die 8 unterschiedlichen Buchstaben im SATOR-Quadrat und in den
beiden gleichen ZW-Hälften des Wortes PENS-ATOR einen
inneren Bezug zu den 4+4 Diagonalpunkten haben. Die ZW des
SATOR-Quadrats zeigen einerseits eine Gemeinsamkeit mit dem 1-25
Numerierungsmodell, andererseits scheinen sie auf dieses abgestimmt zu sein.
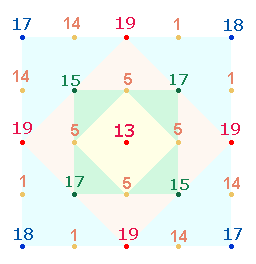
Zunächst sollen die 4+4 Diagonalpunkte addiert werden:
|
|
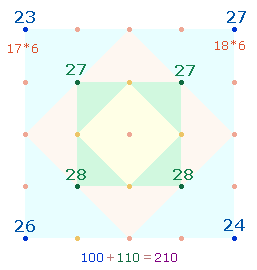
Die Additionen ergeben zwei
Zahlenverhältnisse, einmal zwischen den beiden Quadratrahmen und einmal
zwischen den beiden Diagonalen: 10*(10:11) und 6*(17:18). Die Zahl 210 ist
die Summe der Faktorenwerte der Zahlen von 1-24 und die Umkehrung der Zahlen 102 und
201. Die angrenzenden Zahlen 10 und 11 sind konstitutiv für die Zahl 21 und sind in der Doppelraute durch 10 Linien und 7 Punkte + 4 Dreiecke vertreten. Die
Additionsergebnisse 102 und 108 sind durch den ZW von R und S und durch den gemeinsamen Fator 6 teilbar.
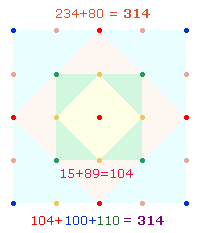
3. Die Zahlenwerte der ersten drei Konstruktionsschritte haben dasselbe
Ergebnis 314 wie die Zahlenwerte des vierten Konstruktionsschritts. Die Zahl 314 ist
bekannt als Faktor p. Diese
Gleichheit entspricht der Grundgleichung 1+2 = 3:
|
|
4. Dieselbe Gleichheit zeigt sich, wenn man die ZW der 4 Quadrate addiert:
|
|
1-25 |
SQ |
Sm. |
|
Qu1 |
79 |
33 |
102 |
|
Qu2 |
115 |
97 |
212 |
|
Qu3 |
129 |
173 |
302 |
|
|
323 |
303 |
626 |
|
Qu4 |
325 |
303 |
628 |
|
|
648 |
606 |
1254 |
Die beiden Ergebnisse zeigen
zwei Möglichkeiten der Bildung einer geraden Zahl, entweder durch zwei Zahlen,
die durch eine mittlere getrennt sind (323-325), oder durch zwei gleiche Zahlen (303-303). Das Endergebnis 1254 hat die Faktoren 2*3*11*19. Die Zahlen 11 und 19 beziehen sich auf die
Doppelzählung von Durchmesser- und Radialelementen im einfachen Kreis (5+6) und im Doppelkreis (9+10)., hier der Kreise um das innere
und äußere Quadrat (nicht die Rautenquadrate). Die Zahlen 2 und 3 können unter anderem
verstanden werden als Radialelemente des äußeren Kreisrings und des inneren
Kreises.
III.
Vergleich des Quadrats mit dem Tetraktysstern
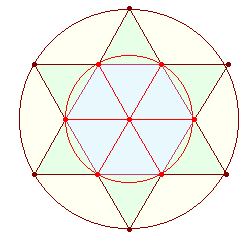
1. Wenn man vom kleinsten Kreis des quadratischen Modells
ausgeht, hat der kleine Kreis des Tetraktyssterns den doppelten Radius und
damit den Flächenwert 4. Da das Verhältnis der beiden Flächen 1:3 beträgt, erhält der äußere Kreis den Flächenwert 12. Die Addition
der Flächeneinheiten ergibt für den Tetraktysstern 16, für das quadratische Modell 15, insgesamt 31.
|
|
|
2. Im ersten Abschnitt wurden die Buchstaben des Wortes
SATOR und deren Zahlenwerte aus Gegebenheiten von Achsenkreuzen abgeleitet. Der
ZW 69 von SATOR setzt sich zusammen aus den 3
Konsonanten STR mit dem ZW 54 und den 2 Vokalen AO mit dem ZW
15. Nun liegt es in der Logik eines zyklischen Systems, daß
die Multiplikation + Addition von zwei Zahlen, deren zweite um einen Zähler
niedriger als die zyklische Gesamtheit ist (10-1=9), zu den beiden
Ausgangszahlen auf zweistelliger Ebene zurückkehrt. Demnach setzt sich 54 aus 6*9 und 15 aus 6+9 zusammen. Beide Zusammensetzungen sind in den Achsen des
Hexagons und des Tetraktyssterns erkennbar: Die 3 Achsen des Hexagons enthalten
je 3*2 = 6 Radiallinien und 3*3 = 9 Punkte (15). Die Erweiterung des Hexagons zum
Tetraktysstern führt zu 3 Doppelrauten mit je 2 Axiallinien, die aus jeweils 9
Durchmesserelementen bestehen. Daraus ergibt sich die Multiplikation 6*9 (54).
Erstellt: September 2001
Letzte Änderung: Dezember 2005