Römischer Würfelturm

im Landesmuseum Bonn

I. DUODECIM SCRIPTA (I)

II. Das Buchstabenquadrat und verwandte Wortgruppen

III. Die Zahlenwerte des Buchstabenquadrats

IV. Beziehungen zum SQ

a) WQ b) Widmung c) PARTHI-Wortgruppe

V. Die geometrischen Modelle

VI. Zusammengesetzte Ergebnisse

VII. DUODECIM SCRIPTA (II)

I. DUODECIM SCRIPTA (I)

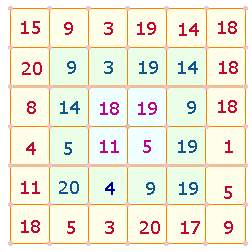
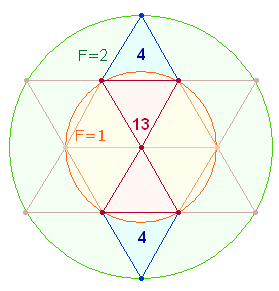
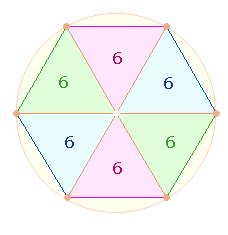
1. Der vorstehende Würfelturm, über den es eine gute Beschreibung im Internet gibt, enthält ein Buchstabenquadrat aus sechs Wörtern. Es bezieht sich auf ein beliebtes römisches Brettspiel, für das die Bezeichnung DUODECIM SCRIPTA – Zwölf Buchstaben überliefert ist, wobei die Bedeutung von SCRIPTA nicht eindeutig geklärt ist; das Wort wird neuerdings auch durch Markierungen wiedergegeben. Eine Lösung wird im letzten Abschnitt versucht. In Wirklichkeit handelt es sich um drei Reihen von je 12 Markierungen, die noch einmal in je 2x6 unterteilt sind. Der Name leitet sich also von 12 Markierungen einer einzelnen Reihe ab, die zweimal wiederholt wird, wie folgende Steinbearbeitung aus Ephesus erkennen läßt:

Die daneben aufgestellten Faltstühle verdeutlichen, daß es sich um ein Spiel für zwei Personen handelt.

Man nimmt allgemein an, daß gewöhnlich Buchstaben die Markierungen ersetzten. Darauf weisen zahlreiche inschriftliche Funde von dreimal zwei untereinander gesetzte Wörter hin. Auch einige Spielbretter mit Wörtern sind gefunden worden. (Quelle) Das folgende aus Ostia enthält für jeden Block dieselben Buchstaben:

C C C C C C	B B B B B B
A A A A A A	A A A A A A
D D D D D D	E E E E E E

Die alphabetische Abfolge zeigt, daß die Spieler in der Mittelreihe begannen und in der angegebenen Folge von einem Sechserblock zum nächsten vorrückten. Die zwei A-Blöcke lassen darauf schließen, daß jeder Spieler seinen eigenen Block in der Startphase hatte. Die Spielregeln sind mehrfach rekonstruiert worden, unter anderem in einer englisch-sprachigen Arbeit von Peter Schamber, die etwa 100 Beispiele von sechs Wörtern enthält.

Auch wenn die Unterteilung der 36 Felder in jeweils 6 eine Numerierung unnötig macht, hat es sie vielleicht ursprünglich gegeben. Da aber Zahlen im römischen Kulturbereich durch ein oder mehrere Buchstaben wiedergegeben werden, bedeuten Wörter aus Einzelbuchstaben statt Zahlbuchstaben eine Vereinfachung. So könnte die Numerierung ein Zwischenschritt zu ganzen Wörtern gewesen sein.

Mehrere archäologische Funde der beschriebenen Spielgestaltung sind in einem russischen Blog enthalten. Eine wissenschaftliche Bearbeitung dieser Funde geht über meine zeitliche Kapazität. Ich beziehe mich im wesentlichen auf Interneteinträge. Mir geht es in erster Linie um die geometrisch-gematrischen Zusammenhänge.

2. Aus Funden weiß man, daß jeder Spieler mit drei Würfeln spielte und 15 plättchenförmige Steine besaß, die auf der einen Seite durchnumeriert waren und auf der anderen Seite mit unterschiedlichen Motiven versehen waren, weswegen man annimmt, daß jeder Spieler seine eigenen Steine einsetzte. (Quelle)

II. Das Buchstabenquadrat und verwandte Wortgruppen

1. Je zwei Wörter des Buchstabenquadrats gehören zusammen:

PICTOS VICTOS	Die Pikten sind besiegt.
HOSTIS DELETA	Die Feindin ist vernichtet.
LUDITE SECURI	Spielt unbesorgt!

Zwei grammatikalische Unregelmäßigkeiten fallen auf: die Akkusativform der ersten Zeile und die feminine Endung der zweiten. Sie erscheinen gerechtfertigt durch das Erfordernis von sechs Buchstaben, das in den korrekten Formen PICTI VICTI und HOSTIS DELETUS nicht erfüllt wäre. Der Plural HOSTES DELETI wäre allerdings möglich gewesen. Die feminine Singularform könnte als Personifikation des Stammes der Pikten verstanden werden. Eine gewisse schöpferische Freiheit in der Bildung der sechs Wörter dürfte allgemein zugestanden worden sein.

Die ersten beiden Aussagen sind durch synonymen Inhalt verbunden, die erste konkret, die zweite allgemein. Die drei Aussagen werden von einem fiktiven Sprecher an die Spieler gerichtet.

Mit PICTI – die Bemalten, Tätowierten bezeichneten die Römer Stämme des heutigen Schottland. Sie machten den Römern im dritten und vierten Jahrhundert sehr zu schaffen, wurden jedoch stets hinter den Hadrianswall zurückgedrängt. Der Würfelturm wird von der Wissenschaft ins späte dritte Jahrhundert datiert.

2. Der Autor der sechs Wörter griff auf bereits bekannte Muster des logischen Ablaufs und der einzelnen Wörter zurück. Am ähnlichsten ist das folgende:

PARTHI OCCISI	Die Parther sind getötet.
BRITTO VICTUS	Der Brite ist besiegt.
LUDITE ROMANI	Spielt, Römer!

Der Autor ersetzte PARTHI durch PICTOS bei gleicher Initiale. PICTOS VICTOS entfaltet eine originelle lautmalerische Wirkung: Ein feindlicher Stamm, der VICTOS in der Lautung fast gleicht, vermittelt den Eindruck eines schwierigen, ja ebenbürtigen Gegners.

Die Römer lieferten sich zahlreiche Kämpfe mit den Parthern. Die Brettspielwörter könnten unter der Herrschaft des Kaisers Marc Aurel in der 2. Hälfte des 2. Jahrhunderts geschaffen worden sein.

Gleich ist auch die Folge von Plural und Singular sowie synonyme Partizipien OCCISI > VICTOS, VICTUS > DELETA; VICTUS ist nach oben verschoben und wird zu VICTOS. Die Aufforderung LUDITE folgt als gemeinsamer Abschluß. Wenn also die Wortgruppe PARTHI OCCISI ... bekannt war, konnte der Autor mit Anerkennung seiner kreativen Weiterentwicklung rechnen.

BRITTO, Genitiv BRITTONIS, ist eine Nebenform für BRITANNUS, ein Bewohner Britanniens. Verwendet wird ein metonymischer Singular

Der Plural HOSTES tritt in zwei Wortgruppen auf:

HOSTES VICTOS	Über die besiegten Feinde
ITALIA GAUDET	freut sich Italien.
LUDITE ROMANI	Spielt, Römer!

Der Akkusativ HOSTES VICTOS ist hier regulär mit dem Verb GAUDET verbunden. Der Autor unserer Wortgruppe könnte die erste Zeile übernommen haben, jedoch ohne grammatische Verbindung zu einem Verb, wie sich auch in der ersten Zeile der folgenden Wortgruppe zeigt.

VIRTUS IMPERI	Tüchtigkeit des Reiches
HOSTES VINCTI	Die Feinde sind gefesselt
LUDANT ROMANI	Die Römer mögen spielen!

Die ersten beiden Wörter bilden keine Aussage, sie bilden das Subjekt eines nicht ausgeführten Satzes.

Auch die Aufforderung LUDITE SECURI hat der Autor der Würfelturmwörter übernommen:

LUDITE SECURI	Spielt unbesorgt,
QUIBUS AESEST	die ihr stets Geld
SEMPER INARCA	in der Kasse habt.

Die Freiheit besteht hier, wie in zahlreichen anderen Fällen, in der Zusammenziehung zweier Wörter aus AES EST und IN ARCA. Wenn der Satz einen Sinn haben soll, müßte wohl übersetzt werden ... solange ihr stets Geld in der Kasse habt.

3. Neben PICTOS ist DELETA inschriftlich nicht belegt. Das Wort leitet geschickt zu LUDITE über, mit dem es vier Buchstaben gemeinsam hat. Das U und I findet sich wiederum in SECURI. Diese auffällige klangliche Verflechtung beginnt mit PICTOS VICTOS und wird durch HOSTIS fortgesetzt. DELETA eröffnet mit Beginn der zweiten Quadrathälfte ein neues Klangbild.

III. Die Zahlenwerte des Buchstabenquadrats

1. Der Hersteller des Würfelturmes war sich der besonderen Bedeutung des Buchstabenquadrates wohlbewußt, sonst hätte er nicht in einem aufwendigen Verfahren die Buchstaben aus einer Kupferplatte ausgestanzt.

2. Urmodell eines jeden denkbaren Buchstabenquadrats ist das SATOR-Quadrat (SQ):

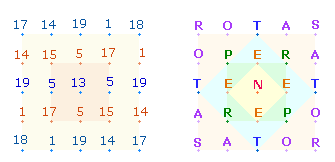
Dem SQ liegt eine komplexe Zahlenkonstruktion zugrunde, die in Buchstaben gemäß ihrer alphabetischen Reihenfolge übertragen wird. Die Reihenfolge dieses Vorgangs ist grundlegend: Wörter erhalten ihre Bedeutung aus geometrischen und numerischen Bedeutungsmodellen.

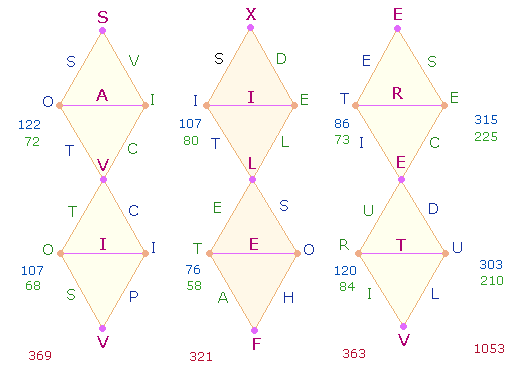
3. Das Verfahren, Buchstaben als Zahlenwerte umzusetzen, nennt man Gematrie. Auch die sechs Wörter des Würfelturms genügen den Bedingungen einer geplanten Zahlenkonstruktion. Die sechs Wörter haben folgende Zahlensummen (ZS):

	PICTOS	VICTOS	HOSTIS	DELETA	LUDITE	SECURI	sm
ZS	78	83	86	45	68	72	432
	7*23		131		7*20
432 = 36*12; 72 = 6*12

Die Zahlensumme 432 bedeutet, das der durchschnittliche Zahlenwert je Buchstabe 12 beträgt. Der Durchschnittswert 12 ist im Wort SECURI allein enthalten, was zur Verstärkung des Sicherheitsgefühls beiträgt. PICTOS hat den durchschnittlichen ZW 13.

Die ZS des ersten und dritten Wortpaares sind durch 7 teilbar und bilden somit einen Rahmen für das mittlere Wortpaar, dessen ZS 131 nach beiden Seiten hin gleich ist.

4. Quadrate können in konzentrischen Rahmen vorgestellt werden, die neben linearen Buchstabenzeilen Ordnungsfunktion haben. Im Fall des SQ besteht der äußere Rahmen aus den Umkehrwörtern SATOR und ROTAS, der innere aus PER und REP. Der Mittelpunkt ist auf jeden Quadratrahmen (QR) beziehbar, der des Würfelturmquadrats (WQ) besteht aus 4 Buchstaben:

Der äußere QR ist in PICTOS und SECURI sowie die verbleibenden 8 vertikalen Buchstaben VHDL und SSAE aufteilbar. Die ZS der beiden Buchstabengruppen sind 150+85 = 5*(30+17) = 235. Die mittleren Buchstaben STLE haben die ZS 53. Zusammen ergibt sich für 12+(8+4) = 24 Buchstaben die ZS 288 = 24*12. Die 24 Buchstaben haben wiederum den durchschnittlichen ZW 12. Wenn also die vier Mittelbuchstaben dem äußeren QR zugeordnet werden, ist das ZS-Verhältnis von 24:12 Buchstaben 12²*(2:1).

Das ZS-Verhältnis der 12:(8+4) Buchstaben ist 150:138 = 6*(25:23).

IV. Beziehungen zwischen dem WQ und dem SQ

a) Das Buchstabenquadrat

1. Die ZS der beiden Quadrate sind 432+303 = 735 = 3*5*7². Die äußeren QR der beiden Quadrate bestehen aus 20+16 = 36 Buchstaben. Auch hier ergibt sich ein erstaunliches ZS-Verhältnis, wenn man die ZS der äußeren Quadratrahmen addiert: 235+206 = 441 = 21² = 3*3*7². Das ZS-Verhältnis der 36:25 Buchstaben beträgt somit 3*7²*(3:2).

2. Im SQ bildet das Wort OPERA (52) die gematrische Verbindung zwischen SATOR (69) und TENET (61): 52:(69+61) = 52:130 = 26*(2:5). Dieses gematrische Verhältnismuster ist auch bei der Zusammenlegung der ZS beider Quadrate gewahrt. Zunächst zeigt sich ein ZS-Verhältnis der äußeren zu den inneren Wörtern:

	ZS		ZS
ROTAS	69	TENET	61
PICTOS	78	HOSTIS	86
SECURI	72	DELETA	45
SATOR	69
	288		192
288:192 = 96*(2:3) = 480

Die ZS und FS von TENET und DELETA, die drei Buchstaben gemeinsam haben, sind jeweils gleich. Eine Angleichung an das SQ bei der Wahl von DELETA ist vorstellbar.

Die übrigen vier Wörter haben die ZS 255. Das ZS-Verhältnis von 7:4 Wörtern beträgt demnach 480:255 = 15*(32:17).

b) Die Widmung

1. Auf drei Seiten am oberen Rand ist eine Widmung aus drei Wörtern herausgearbeitet:

UTERE FELIX VIVAS

Benütze – glücklich – du mögest leben

Die drei Wörter bestehen aus je fünf Buchstaben. Wörter der Gemütsbewegung und der Befindlichkeit (SECURI) werden prädikativ, also ohne Adverbendung verwendet. Das Adjektiv FELIX kann sowohl dem ersten als auch dem dritten zugeordnet werden. Beides ist inschriftlich belegt. Die Übersetzung kann also heißen: Benütze den Würfelturm glücklich und Lebe glücklich.

2. Im System römischer Gematrie werden nicht nur die Zahlenwerte (ZW), sondern auch deren Faktorenwerte (FW) gezählt. Von den Zahlensummen (ZS) und den Faktorensummen (FS) lassen sich dann wieder die FW bestimmen. Für die Widmung sind diese "4Werte" von einer gewissen Bedeutung:

	ZS	FS	sm	FW1	FW2	sm	GS
UTERE	66	55	121	16	16	32	153
FELIX	52	37	89	17	37	54	143
VIVAS	68	33	101	21	14	35	136
	186	125	311	54	67	121	432

Die Gesamtsumme 432 entspricht der ZS des Buchstabenquadrats. Auf diese Weise werden die drei Wörter der Widmung mit den sechs Wörtern des Quadrats inhaltlich miteinander verbunden. Dies geschieht auch umgekehrt. Denn die Addition 186+432 führt zur Umkehrzahl 618 = 6*103. Die Zahl 6 im Zusammenhang mit dem Würfelspiel bezieht sich wesentlich auf die sechs Seiten eines Würfels. Das Verhältnis der Summen 153:136 beträgt 17*(9:8). Es handelt sich um die Summen der Zahlen 1-17 und 1-16.

Die 4Werte des Buchstabenquadrats sind:

	ZS	FS	sm	FW1	FW2	sm	GS
PICTOS	78	53	131	18	53	71	202
VICTOS	83	54	137	83	11	94	231
HOSTIS	86	56	142	45	13	58	200
DELETA	45	45	90	11	11	22	112
LUDITE	68	54	122	21	11	32	154
SECURI	72	48	120	12	11	23	143
	432	310	742	190	110	300	1042

Die 4Werte-Summe der 6+3 Wörter beträgt 1042+432 = 1474 = 11*134 = 22*67. Vier Summen sind durch 11 teilbar, wodurch sich ein Verhältnis der 4:5 Wörter von 11*(61:73) ergibt. Die beiden Adjektive SECURI und FELIX haben jeweils dieselbe Gesamtsumme 143 = 11*13 und werden damit eng miteinander verbunden.

Die ZS+FS der 9 Wörter beträgt 742+311 = 1053 = 81*13 = 9*117. Die ZS+FS je Wort ist also 117 = 9*13.

3. Das vermittelnde Wort FELIX hat dieselbe ZS 52 wie OPERA. OPERA FELIX könnte heißen Wirke glücklich. Die drei Wörter der Widmung übernehmen den zweiten Teil des SQ . Zusammengesetzt ergeben sich folgende ZS+FS:

	ZS	FS	sm
ROTAS	69	54	123
OPERA	52	40	92
TENET	61	61	122
UTERE	66	55	121
FELIX	52	37	89
VIVAS	68	33	101
	368	280	648
280:368 = 8*(35:46) = 8*81
104:264 = 8*(13:33)
77:203 = 7*(11:29)

Die Summen der Wörter TENET UTERE bilden mit den übrigen 4 Summen das ZS+FS-Verhältnis 243:405 = 81*(3:5).

4. Zur Vollständigkeit gehören noch die 4Werte des SQ:

	ZS	FS	sm	FW1	FW2	sm	GS
ROTAS	69	54	123	26	11	37	160
OPERA	52	40	92	17	11	27	120
TENET	61	61	122	61	61	122	244
sm	182	155	337	104	83	187	524
AREPO	52	40	92	17	11	27	120
SATOR	69	54	123	26	11	37	160
GS	303	249	552	147	105	252	804
804 = 12*67

Die 4Werte des SQ und des WQ haben denselben Faktor 67. Das Verhältnis beträgt 134*(6:11) = 2*17*67 = 2278. Es sei hier schon erwähnt, daß sich unter der Widmung, die sich über drei Turmseiten erstreckt, jeweils ein Rechteck aus 6*7 ausgestanzten Öffnungen befindet.

c) Die PARTHI-Wortgruppe

1. Das SQ ist von höchster religiöser Relevanz. Es beinhaltet nichts weniger als die Vorstellung einer Gemeinschaft von drei göttlichen Personen. Seine Wirkungsdauer ist erstaunlich, wenn man bedenkt, daß sich das Christentum stetig ausbreitete und andererseits Mysterienkulte wie der Mithraskult viele Anänger hatte. Drei Gründe können vielleicht angeführt werden. Erstens, das SQ ist unlöslich mit der Romidee verbunden, die als festgefügt und unabänderlich empfunden wurde. Zweitens, insofern das Christentum als Konkurrent zur Romidee betrachtet wurde, galt es, deren Sinnstruktur als Gegengewicht am Leben zu erhalten. Drittens, das Brettspiel duodecim scripta hatte eine lange Tradition, deren Gestaltungsmuster weitergeführt wurden. Zu ihnen gehören offensichtlich Schöpfungen von sechs Wörtern, die gematrisch mit dem SQ zusammenstimmen. Die gematrische Überprüfung ist nicht leicht, da die Konvergenzbereiche verschieden sein können und teils mühsam aufgesucht werden müssen. Da der Schöpfer des WQ sich am engsten an die PARTHI-Wortgruppe anlehnt, soll deren gematrische Relevanz untersucht und damit aufgezeigt werden, daß das WQ zwar einzigartige Konstruktionsmerkmale aufweist, diese aber auch in vergleichbaren früheren Beispielen zu finden sind.

2. Die 4Werte der 6 Wörter des Parther-Quadrats (PQ) sind:

	ZS	FS	sm	FW1	FW2	sm	GS
PARTHI	69	57	126	26	22	48	174
OCCISI	56	35	91	13	12	25	116
BRITTO	80	72	152	13	12	25	177
VICTUS	89	54	143	89	11	100	243
LUDITE	68	54	122	21	11	32	154
ROMANI	66	53	119	16	53	69	188
	428	325	753	178	121	299	1052
428 = 4*107; 325 = 13*25; 753 = 3*251
1052 = 4*263; 174:116 = 2*29*(3:2)

Die FS 325 hat Bezug zu den 25 Buchstaben des SQ, insofern sie die Summe der Zahlen von 1-25 ist. Die FS der 20 Buchstaben des Quadratrahmens und der 16 Buchstaben des inneren Quadrats haben das Verhältnis 169:156 = 13*(13:12), die entsprechenden ZS das Verhältnis 228:200 = 4*(57:50) = 4*107. Das letztere ist insofern von Bedeutung, als 57 und 50 die ZS und FS des Wortes PATER sind. Davon sind vier Buchstaben bereits in PARTHI enthalten, das fehlende E findet sich in LUDITE. Das ZS-Verhältnis von 31:5 Buchstaben ist demnach 107*(3:1).

PARTHI hat dieselbe ZS 69 wie SATOR – Schöpfer. PARTHI und ROMANI korrespondieren durch 69:66 = 3*(23:22) und 126:119 = 7*(18:17) = 245. Die entsprechende Summe des SQ ist die angrenzende Zahl 246.

3. Die Hinzufügung der SQ-Werte führt zu einer durchschaubaren Ordnung von Zahlenverhältnissen:

	ZS	FS	sm	FS1	FS2	sm	GS
PQ	428	325	753	178	121	299	1052
SQ	303	249	552	147	105	252	804
	731	574	1305	325	226	551	1856
731 = 13*43; 574 = 14*41
551:1305 = 29*(19:45)
731+325 = 1056; 574+226 = 800
800:1056 = 32*(25:33)

Wie die 11 Wörter gruppiert werden können, um Zahlenverhältnisse zu ermöglichen, soll an den ZS+FS und den 4Werten gezeigt werden:

ROTAS	123	OCCISI	91	PARTHI	174	ROTAS	160
PARTHI	126	BRITTO	152	OCCISI	116	AREPO	120
OPERA	92	TENET	122	BRITTO	177	OPERA	120
AREPO	92	VICTUS	143	VICTUS	243	TENET	244
ROMANI	119	LUDITE	122	LUDITE	154	ROMANI	188
SATOR	123			SATOR	160
	675		630		1024		832
675:630 = 45*(15:14)				1024:832 = 64*(16:13)

4. Nur etwa ein halbes Dutzend der bisher gefundenen Wortgruppen enthält einen militärischen Bezug. Der Schöpfer der PARTHI-Wortgruppe dürfte dieses thematische Muster bereits gekannt haben, da anzunehmen ist, daß die Urfassung eher allgemein gehalten war, also nicht einen Feind beim Namen nannte. Sein gematrisches Vorgehen ist von den Ergebnissen ablesbar: Er erkennt die gemeinsame ZS 69 von PARTHI und SATOR und ermittelt 174 als 4W-Summe. Er sucht ein passendes Partizip und findet in OCCISI die 4W-Summe 116, die wie 174 ebenfalls durch 29 teilbar ist; beide Summen sind durch 10 teilbar. Dazu findet er ein paralleles Paar mit Teilbarkeit durch 10.

Nun stimmt er sein eigenes Quadrat mit dem SQ so ab, daß sowohl die vereinten ZS+FS als auch die FW1/2-Summen durch 29 teilbar sind. Es gelingt ihm sogar ein gemeinsamer Teiler von ZS+FW1-Summe und FS+FW2-Summe, was als eine Besonderheit zu gelten hat.

Die Überlegung hinter all dem ist, daß zwei gematrisch gleiche Mächte, SATOR und PARTHI, die eine göttlich, die andere irdisch, einander gegenüberstehen, daß aber die Römer die göttliche Macht auf ihrer Seite haben und durch 64*29 den Sieg erringen; denn die 4W-Summe von SATOR ROTAS ist 320 = 5*64.

V. Die geometrischen Modelle

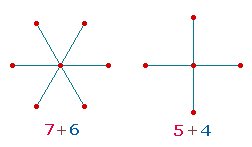
1. Römisches Denken war geprägt von geometrischen Modellen. Im Kern geht es um zwei Achsenfiguren, einer dreiachsigen und zweiachsigen:

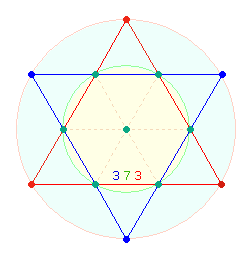
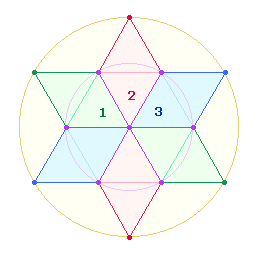
Die dreiachsige Figur entwickelt sich über das Hexagon zum Tetraktysstern, die zweiachsige zum Quadrat. Im Tetraktysstern sind zwei Figuren erkennbar, eine zweifach (Tetraktys), die andere dreifach (Doppelraute):

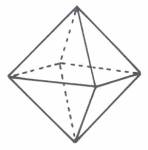
Zwei Doppelrauten (DR) können ein Achsenkreuz bilden und zu einem Oktaeder zusammengefügt werden:

Einem Würfel liegt zwar ein Quadrat zugrunde, aber er kann daraus nicht entwickelt werden wie ein Oktaeder. Beide dreidimensionale Figuren sind jedoch insofern verwandt, als sie jeweils aus 26 Elementen bestehen, wobei Ecken und Flächen vertauscht sind: Der Oktaeder hat 6 Ecken und 8 Flächen, der Würfel 8 Ecken und 6 Flächen. Beide haben 12 Kanten.

2. Das Brettspiel duodecim scripta verbindet in allgemeiner Weise beide Achsensysteme, deren Endfiguren der Oktaeder und der Würfel sind. Im besonderen werden auch die beiden Tetraktys und die drei DR verbunden: Die Numerierungssumme von 6 Würfelflächen ist 21, der ebenso viele Elemente der DR entsprechen. Auf 21 Elemente kommt auch der Rahmen einer Tetraktys, wenn von jeder Seite 4 Punkte und 3 Linien gezählt werden. Auf diese Weise herrscht Gleichheit von 42 Elementen bei zwei Tetraktysrahmen und zwei DR, die einen Oktaeder bilden. Die Tetraktys- und DR-Paarung legen ein Spiel zu zweit nahe.

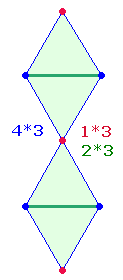
Ohne Einzelzählung jeder Tetraktysseite besteht ein Tetraktysrahmen aus 9 Punkten und 9 Linien, also aus 18 Elementen, die sich mit der zweiten Tetraktys auf 36 verdoppeln. Diesen 36 Elementen entsprechen je 12 Elemente der drei DR, die sich aus 4*3 "Dachelementen" zusammensetzen:

Drei Dachelemente bestehen aus zwei Linien und einem Punkt in der Mitte.

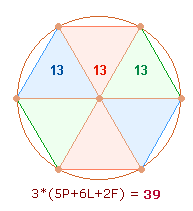
Wenn jede DR mit jeder ein Achsenkreuz bilden, um zu einem Oktaeder zusammengefügt zu werden, sind es drei DR-Kreuze und 3*42 = 126 Elemente. Diese werden durch ein Rechteck von 6*7 Reihen dargestellt, auf jeder der drei Platten zweimal, sodaß die Summe die doppelte Zahl 252 beträgt. Passenderweise besteht der rechteckige Rahmen jeweils aus Rauten.

Der DR-Rahmen besteht aus 8 Linien und 7 Punkten, denen die Buchstabenzahl des Namens duodecim scripta entspricht. Diese 15 Elemente könnten als Modell für die Verwendung von 15 Spielsteinen gedient haben.

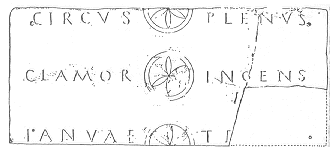
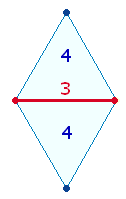
Charakteristisch für die aufgefundenen Tafeln ist, daß die Mitte zwischen zwei Wörtern oder 6-er Feldern durch einen Kreis mit Schnittpunkt wiedergegeben wird, der volle Kreis jedoch nur der mittleren Linie zugestanden ist, während die Trennungsmarkierungen der äußeren Linien Halbkreise darstellen, wie ein Beispiel aus dem Britischem Museum zeigt:

Es dürfte einleuchten, daß die beiden Halbkreise zusammen einen ganzen Kreis ergeben, d.h. daß zwei der drei DR ein Achsenkreuz bilden. Die Rosette innerhalb zweier Kreisringe stellt in anschaulicher Stilisierung drei DR dar.

3. Die 4*3 Elemente des DR-Rahmens können schleifenförmig mit Buchstaben besetzt werden. Wenn der Autor des Buchstabenquadrats diesen Zusammenhang kannte, wird er darin einen Prüfstein der Vollkommenheit seines Werkes erkannt und die sechs Wörter daraufhin geprüft haben, wie es im folgenden geschieht:

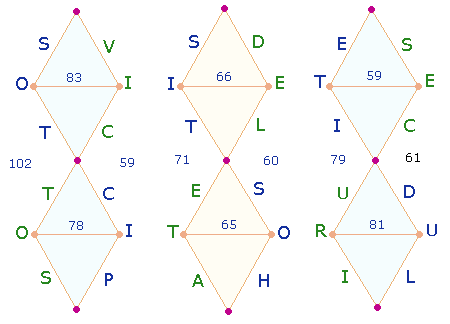
Jede Schleife beginnt unten, der erste (blaue) Buchstabe rechts. Die sechs Buchstaben eines Wortes besetzen zwei Rautenhälften.

Zwei Verhältnisse von ZS sind denkbar: die ZS der unteren und oberen Rauten und der linken und der rechten vertikalen Seiten. Das ZS-Verhältnis der unteren zu den oberen Rauten ist 224:208 = 16*(14:13), das Verhältnis der linken zu den rechten Seiten 252:180 = 36*(7:5).

4. Die drei Wörter der Widmung sind ebenfalls in den DR unterzubringen, auf den drei Vertikalpunkten und den zwei Querlinien. Die normale Zuordnung würde sich nach der Reihenfolge beider Wortgruppen richten. Die befriedigenderen Summen kommen aber zustande, wenn man UTERE mit dem letzten Wortpaar LUDITE SECURI verbindet. Hier wird man auch die FS hinzunehmen, da die ZS+FS 1053 durch 3⁴ teilbar ist:

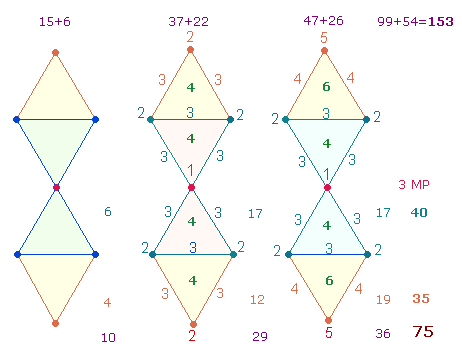
Die drei Mittelpunktbuchstaben VLE sind den oberen Rauten zugeordnet. Alle Einzelsummen sind durch 3 teilbar. Das ZS+FS-Verhältnis der unteren zu den oberen Rauten beträgt 513:540 = 27*(19:20), das FS-Verhältnis 210:225 ist 15*(14:15), das FS:ZS-Verhältnis der oberen Rauten 15*(15:21).

Auch die ZS+FS der Querlinien und ihrer seitlichen Punkte sind durch 9 teilbar:

	ZS	FW	sm
OII-TEO-RTU	126	99	225
OAI-IIE-TRE	88	74	162
162:225 = 9*(18:25) = 387
387:666 = 9*(43:74)

5. Die gematrischen Eigenschaften der Wörter LUDUS und LUDERE selbst weisen auf die DR hin:

	L	U	sm	D	sm	U	S	sm	GS
ZW	11	20	31	4	35	20	18	38	73
FW	11	9	20	4	24	9	8	17	41
			51		59			55	114

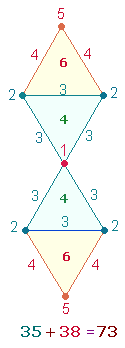
Die Einzelziffern der Zusammensetzung LU+D des Wortstammes ist als Gleichung 3+1 = 4 auf jeweils 4 Punkte einer Raute interpretierbar. Die Zahl 1 bedeutet hier einen zusätzlichen Mittelpunkt. Zwei Rauten legen zwei Spieler nahe. Die ZS 35 und ZS+FS 59 bedeuten dasselbe: das Kreisflächenverhältnis 1:3 der beiden Tetraktyskreise, einmal wiedergegeben durch 3:5 Radialelemente und einmal durch 5:9 Durchmesserelemente. Auch die Faktoren 5*7 der ZS 35 haben dieselbe Bedeutung, da der hexagonale Bereich der DR aus 5 und die ganze DR aus 7 Punkten besteht. Die ZS 73 ist am einfachsten auf 7+3 Tetraktyspunkte zu beziehen, aber auch auf ein Numerierungsmodell, das für die 21 Elemente der DR die Summe 73 ergibt:

Aus der Grafik ist ersichtlich, daß die Aufteilung der Numerierungssumme in den hexagonalen und Erweiterungsteil genau der ZS von Wortstamm und Endung von LUDUS entspricht.

Die FS 41 ist in der DR durch die Elemente von drei geometrischen Figuren vertreten:

Außerdem besteht ein DR-Kreuz aus 41 Elementen.

Die ZS von LUDERE ist 62. Die Einzelziffern lassen sich wiederum auf zweimal 3+1 Rautenpunkte beziehen.

Auch die Bezeichnung duodecim scripta für das Würfelspiel zeigt Bezüge zur DR:

	ZS	FS	sm	FW1	FW2	sm	GS
duodecim	71	47	118	71	47	118	236
scripta	82	62	144	43	33	76	220
	153	109	262	114	80	194	456

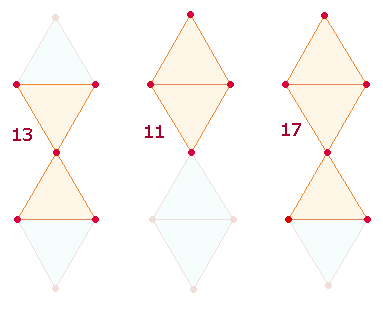
Die ZS 153 entspricht drei Zählungen der DR, einer unnumerierten und zwei numerierten:

Die erste Summe betrifft den Rahmen, die zweite die Binnenelemente.

VI. Zusammengesetzte Ergebnisse

1. Zwei Ergebnisse, jeweils durch 81 teilbar, sind bisher noch nicht koordiniert worden: die ZS+FS der 9 WT-Wörter und der 6 Wörter, die sich aus der Widmung und einer Hälfte des SQ zusammensetzen. Es sind die Summen 1053+648 = 81*(13+8) = 81*21 = 1701. Sie können erst jetzt, nach Einführung der geometrischen Modelle, berücksichtigt werden. Aus 13 Elementen besteht das hexagonale Doppeldreieck und aus 2*4 Elementen die Erweiterung der DR:

Aus der Grafik ist auch zu erkennen, daß der DR-Rahmen aus 9 hexagonalen und 2*3 Erweiterungselementen besteht. Der gemeinsame Teiler 81 = 9*9 gibt einerseits zweimal 9 Durchmesserlemente der beiden Zickzacklinien, die die DR bilden, wieder, andererseits deren 2*4 symmetrischen Elemente und den Mittelpunkt. Als reale Zahl bezieht er sich auf ein 5*5 Punkte-Quadrat des SQ, das aus (25 Punkten + 16 Einzelquadraten) + 40 Linien zusammengesetzt ist.

2. Der gemeinsame Teiler 81 erhält dadurch zusätzliches Gewicht, daß die (6+3)+(3+3) = 15 Wörter aus 81 Buchstaben bestehen. Damit hat jeder Buchstabe den durchschnittlichen ZW+FW 21.

Höchst erstaunlich ist, daß auch die beiden FW1/2-Summen der 15 Wörter zusammen durch 81 teilbar sind: (300+121)+(187+121) = 421+308 = 729 = 27*27 = 9*81. Somit ist das Verhältnis der ZS+FS zu den FW1/2-Summen 1701:729 = 243*(7:3). Das Verhältnis 7:3 ist am naheliegendsten auf 10 Tetraktyspunkte zu beziehen, die aus 7 hexagonalen und 3 Erweiterungspunkten bestehen. Die Einzelziffern des gemeinsamen Teilers 243 geben die 3 verschiedenen Elemente der DR-Mitte wieder: 2 Querlinien, 4 Dreiecksflächen, 3 Punkte. Der Potenzausdruck 3⁵ ist wiederum auf 15 Elemente des DR-Rahmens beziehbar, insofern zu 4*3 Dachelementen noch 3 Punkte hinzukommen. 3⁵ kann auch als 3:5 Radialelemente der zwei Tetraktyskreise verstanden werden, denen das Kreisflächenverhältnis 1:3 entspricht.

Die Zahl 81 gibt durch den Potenzausdruck 3⁴ die 4*3 Dachelemente des DR-Rahmens eindrucksvoll wieder. Die Zahl 243 ist daher als 3*3⁴ zu verstehen.

3. Die Widmung nimmt die Funktion einer Vermittlung zwischen dem WQ und dem SQ wahr: Der Spieler kann ohne Sorgen und glücklich sein, wenn er der Aussage des SQ vertraut: Der Schöpfer erhält seine Werke.

4. Nun ist noch das ganze SQ hinzuzufügen: Die 4W-Summen der 9+5+6 Wörter sind 1474+804+(524+432) = 3234 = 66*49. Aus 49 Elementen besteht der Tetraktysstern, in dem sich 6 Rauten aus je 11 Elementen befinden. Die Einzelziffern der nunmehr 106 Buchstaben, aufgeteilt in 53+53, sind wie bei 3⁵ auf die Radialelemente der beiden Tetraktyskeise beziehbar.

VII. DUODECIM SCRIPTA (II)

1. Die Herkunft und der Name des Spiels von 6x6 Feldern ist bisher in der Wissenschaft nicht geklärt. Das Wort SCRIPTUM in Verbindung mit DUODECIM SCRIPTA wird in den traditionellen Lexika wie Menge-Güthling und Der Kleine Stowasser mit Linie übersetzt. Wenn DUODECIM SCRIPTA nicht ein hochrespektables Spiel gewesen wäre, hätte es weder Cicero noch Quintilian zitiert. Cicero wird bei Nonus S.170 zitiert:

Itaque tibi concedo, quod in duodecim scriptis solemus, ut calculum reducas, si te alicuius dati poenitet.

Ich gestehe dir zu, daß du, wie wir es im Spiel DUODECIM SCRIPTA gewohnt sind, den Stein zurückziehst, wenn dich ein Zug reut.

Bei Quintilian Inst. Or. XI, 2,38 heißt es:

An vero Scaevola in lusu duodecim scriptorum, cum prior calculum promovisset essetque victus, dum rus tendit, repetito totius certaminis ordine, quo dato errasset recordatus, rediit ad eum, quocum luserat, isque ita factum esse confessus est?

Scaevola hat ja einmal, als er beim Spiel DUODECIM SCRIPTA den ersten Zug hatte und die Partie verlor, während er aufs Land fuhr, die ganze Partie noch einmal nachgespielt, kehrte, als er sich erinnerte, wo er den Fehler gemacht hatte, zu seinem Spielpartner zurück, und dieser gab ihm zu, so sei es wirklich gewesen.

2. Ich habe oben die 6x6 Felder von den den 36 "Dachelementen" der drei Doppelrauten (DR) abgeleitet. Dies bedarf weiterer Überlegungen: Die Tetraktys läßt die Zahl 10 an der Summe der Punkte 1+2+3+4 ablesen. Jede der 3 Tetraktysseite besteht aus 4 Punkten. Nun kommen die Zahlen 1-4 wiederum durch die Gleichung 3*4 = 12 zustande. Auf diese Weise erhält die Zahl 12 eine besondere Bedeutung. Da im Zahlensystem eine überlegene Ordnung herrscht, lassen sich 2x2 Ziffern zu einer vierstelligen Zahl zusammensetzen und von ihr und ihrer Umkehrung die Faktorenwerte (FW) ermitteln:

Zahl	FW
3412	857
1243	619
4646	1476
1476 = 36*41

Für die 4*3 Dachelemente ist die Zahlenfolge umzukehren:

			sm	FW
Zahl	4312	1243	5555	117
Fkt.	11*392	11*113
FW	31	124	155	36
FW	31:124 = 32*(1:4)			153
117:36 = 9*(13:4)

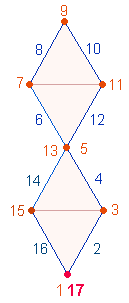
Der FW 36 und die Summe 153 geben einen wichtigen Hinweis auf die Idee des Spiels: Die Zahl 153 ist die Summe der Zahlen 1-17, mit denen der DR-Rahmen schleifenförmig numeriert werden kann:

Wie aus der Grafik zu ersehen ist, ergänzen sich je zwei horizontale Zahlen zu 18. Statt der Zahlen könnten auch Buchstaben in alphabetischer Reihenfolge stehen. Von den 17 Zahlen oder Buchstaben entfallen die 5 der drei vertikalen Punkte. Somit bedeutet DUODECIM SCRIPTA eine Teilsumme von 17, eben 4*3.

3. Die zwei vierstelligen Zahlenpaare haben die Summen 4646 = 46*101 und 5555 = 55*101. Nun sind die Zahlen 55 und 46 die ZS und FS der Zahlen 1-10. Ihre Summe ist 101 und die Faktoren beider vierstelliger Summen daher 101*101 = FW 202:

			sm	FW
Zahl	4646	5555	10201	202
FW	126	117	243	15
FW	126:117 = 9*(14:13)			217

Die 4W-Summen der zusammengesetzen 81 Buchstaben beträgt, wie oben ermittelt, 2430. Ob ein innerer Zusammenhang zur Summe 243 besteht, kann nicht beantwortet werden.

Die Primzahl 101 ist als 10+1 zu interpretieren, zweimal 101 ist auf eine hexagonale Doppelraute beziehbar:

Zwei Rauten, durch den gemeinsamen Mittelpunkt miteinander verbunden, stehen einander in Gleichheit gegenüber. Es bleiben 4 Elemente zur Vervollständigung des Hexagons übrig. Auf göttlicher Ebene wird durch diese Sichtweise das Urbild und das Abbild, die erste und zweite Person, hervorgehoben, die dritte Person fügt sich durch die verbleibenden Elemente ein. Der menschlichen Ebene entsprechen zwei Spieler, deren Reihenfolge vor dem Spiel zu ermitteln ist. Das hexagonale Muster stimmt mit dem PATERNOSTER-Kreuz des SQ darin überein, daß beide Rauten die 21 Buchstaben des PN-Kreuzes aufnehmen und die übrig bleibenden zweimal A O den 4 restlichen Elementen zugeteilt werden. Weiterhin haben die Wörter OPERA TENET die ZS+FS 214. Die beiden Wörter können von TENET aus zweimal gezählt werden, die doppelte Summe 428 stimmt mit der ZS der PARTHI-Wörter überein. Die Zahl 421, zusammengesetzt aus 4+21, ist die FW1/2-Summe der 9 Wörter des Würfelturms.

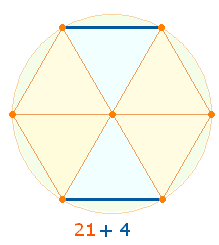
Das Modell 21+4 ist zu ergänzen durch drei sanduhrförmige Doppeldreiecke, die die Gleichheit der drei göttlichen Personen betonen:

Ein einzelnes Dreieck besteht aus 7 Elementen. Läßt man den Mittelpunkt weg, der durch das Modell 21+4 bereits einmal berücksichtigt wurde, erhält man für jedes Doppeldreieck die Folge 6+6. Alle aufgefundenen Zeichnungen trennen zweimal 6 Felder durch kreisähnliche Markierungen, die den Mittelpunkt eines Kreises bezeichnen. Diese Anlage von 6x6 symmetrische hexagonale Elemente sind dann auf die Dachelemente der drei Doppelrauten übertragen worden. Den mittleren Markierungen entsprechen drei Würfel:

4. Die weiter oben ermittelten FW-Summen können wiederum miteinander verrechnet werden:

			sm	FW	sm
FWS	1476	155	1631	240
FW	51	36	87	32
			1718	272
FW			861	25	886

Die Zahl 272 ist die ZS+FS der Zahlen 1-17: 153+119. Die Einzelziffern von 886 = 2*443 weisen auf die DR hin, die aus zwei Rauten mit je 11 Elementen besteht:

5. Ovid hat in der ars amatoria III, 363-364 das Brettspiel so beschrieben:

Est genus, in totidem tenui ratione redactum

Scriptula, quot menses lubricus annus habet:

Es gibt ein Spiel, das in genauer Anordnung in so viele Zeichen

aufgeteilt ist, wie das flüchtige Jahr Monate hat.

Ovid kannte die genauen Zusammenhänge, wie sich den Zahlenwerten entnehmen läßt. Von Bedeutung sind hier die Verse 363 = 3*11*11 und 364 = 2*182. Deren FW sind 25 und 24, sodaß die Summe aus Zahl und FW jeweils 388 = 4*97 = FW 101 beträgt. Es geht einmal um die Gleichheit der Spielchancen, die sich im Quadrat 101² bereits gezeigt haben. Dann aber werden 3 DR aus je 11*11 mit zwei Hälften des SQ verbunden, deren ZS aus 2*182 besteht. Die Gleichheit hat Ovid auch durch gleiche Buchstabenzahl 37 des Distichons dargestellt, was nicht einfach ist, da der Pentameter kürzer als der Hexameter ist. Aus 37 Elementen besteht die Tetraktys.

Der Plural SCRIPTULA ist die Verkleinerung von SCRIPTA. Die ZS 31 der Silbe -UL- ist gleichzeitig die Differenz der FS zur ZS 113, d.h. die ZS 82 von SCRIPTA ist auch die FS von SCRIPTULA. Die Zahl 113 ist einerseits Faktor der Zahl 1243 (11*113) ist. Vielleicht wichtiger ist, daß 113 die ZS von OPERA TENET – er erhält seine Werke ist und die 4W-Summe 364 mit der Zeilennummer übereinstimmt:

	ZS	FS	sm	FW1	FW2	sm	GS
OPERA	52	40	92	17	11	28	120
TENET	61	61	122	61	61	122	244
	113	101	214	78	72	150	364

Es mag Zufall sein, daß die ZS von PICTOS SECURI den Summen 78 und 72 entsprechen.

Die Zeilennummer 363 kann als 36+3 verstanden werden, also 36 Felder und 3 Würfel. Letztere kann man auch zu den zweimal 15 = 30 Spielsteine hinzuzählen. Die Addition 36+33, die ZS+FS der Zahlen 1-8, ergibt die ZS von SATOR. Hinzu kommen zwei Spieler. Die Gesamtsumme 71 läßt sich zusammensetzen aus 17+3 = 20 und 17*3 = 51: 2 Spieler + 15 Steine + 3 Würfel und 36 Felder + 15 Steine.

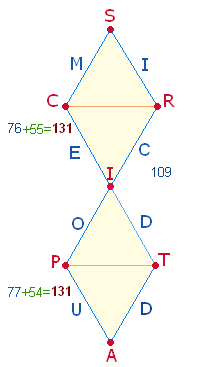
6. Die Bezeichnung DUODECIM SCRIPTA besteht aus 15 Buchstaben, die man auf den Linien und den Punkten des DR-Rahmens anordnen kann. Die ZS+FS der beiden Wörter ist 153+109 = 262:

DUODECIM ist von unten nach oben, SCRIPTA von oben nach unten geschrieben. Wenn man das Mittelpunkt-I der oberen Hälfte zuteilt, ist die ZS+FS der beiden Hälften jeweils 131.

Erstellt: Juni 2013

Start

Inhalt