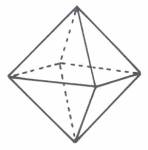
Dezimalmodell OKTAEDER

Die Bedeutung der Zahlen 224 und 242

I. Einleitung

II. Bedeutung der Zahlen 224 und 242

III. 224-242 und 12-21 in der Konzeption des Horaz

IV. Die Zahlen 2 und 3 in Tetraktysstern und Oktaeder

I. Einleitung

1. Das korrekte Genus für Oktaeder ist das Neutrum, also "das Oktaeder". Als ich dies das erste Mal bemerkte, hatte ich schon einige Jahre das Maskulinum "der Oktaeder" gebraucht. Ich sehe im nachhinein allerdings keine Veranlassung, mich umzustellen, da es durchaus Gründe für eine Abweichung vom griechischen Ausgangsgenus gibt. Das lateinische Wort CORPUS ist ebenfalls ein Neutrum, man verwendet im Deutschen aber das Maskulinum. Nun handelt es sich beim Oktaeder um einen dreidimensionalen Körper. Endungen auf –er sind vorwiegend maskulin. Das deutsche Wort für Oktaeder ist "Achtflächner", natürlich der Achtflächner.

Auch sonst gibt es unterschiedlichen Genusgebrauch: Man sagt zwar das Thermometer, aber der Kilometer, obwohl griechisch metron neutrum ist.

Fazit: Nicht immer ist die korrekte Form auch die bessere.

2. Die Mathematik kennt 11 Oktaedernetze. Es handelt sich um die Auffaltung der 8 Flächen, wie im folgenden Beispiel:

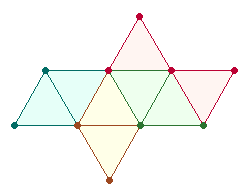
Die 8 zusammenhängenden Flächen haben in sich keine Bedeutung, sie genügen der Bedingung zusammenhängender Flächen, die eine Zusammensetzung zu einem Oktaeder ermöglichen. Anders ist es bei einer Figur, die aus der Entwicklung des Kreises und des Hexagons zum Tetraktysstern erwächst:

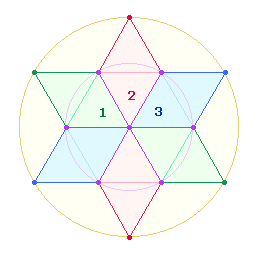
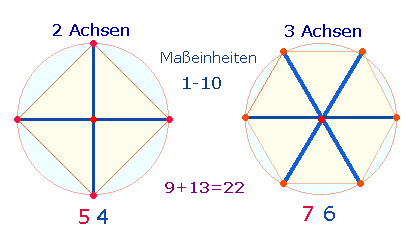
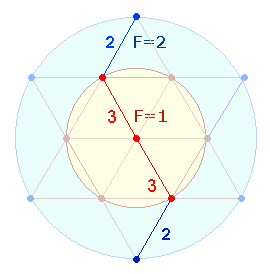
Man erkennt drei Doppelrauten (DR) mit je vier Flächen. Bildet man aus zwei DR ein Achsenkreuz, kann man durch Faltung der Querlinien und Drehung um den Mittelpunkt die 4 Endpunkte zu einem Oktaeder zusammenführen:

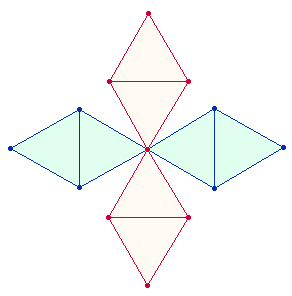
Die Besonderheit dieser Figur besteht darin, daß bei der Bildung des Oktaeders zwei Achsenkreuze aus 3 und 2 Achsen zusammenwirken und diese 10 Maßeinheiten enthalten:

3. Als dreidimensionaler Körper bildet der Oktaeder den Endpunkt der Entwicklung des Dezimalsystems aus dem Kreis, dem Hexagon und dem Tetraktysstern. Daher gehört der Oktaeder zu den Modellen des Dezimalsystems, auf die sich die Grundbedeutungen der Zahlen beziehen. Dazu gehören die Numerierungen 23/24 und 0/10 der Rahmenelemente des DR-Kreuzes.

Die Bedeutungen der Zahlen haben ihren letzten Grund in der Formel des einen Gottes in drei Personen. Unter diesem Gesichtspunkt ist auch der Oktaeder zu sehen.

4. In der Erkenntnis der Zahlenbedeutungen gibt es verschiedenen Ebenen und Abstraktionsstufen. Die Zahlen 3 und 5 beispielsweise sind grundlegende Bestandteile der Kreisachse, die sich im Tetraktysstern und im Oktaeder fortsetzen. Die Wiederkehr grundlegender Zahlen auf einer höheren Ebene ist eine verläßliche Konstante. Sie spornt menschlichen Geist und Willen an, nicht auf einer erreichten Ebene als höchster Sinnstiftung zu verharren, sondern bekannte Elemente und Prinzipien auf einer höheren Ebene wiederzufinden.

Die Zahlenbedeutungen auf den verschiedenen Ebenen zu erfassen, ist ein Vorgang, der durch einen Aufstieg der Erkenntnis zu leisten ist. Dieser Aufstieg zum Absoluten hin ist einerseits Selbstzweck und Aufgabe menschlicher Geistesnatur, andererseits führt sie zu immer größerer innerer Freiheit. Auf einer anderen Erkenntnisebene zu verharren als der, bis zu der menschlicher Geist aufzusteigen vermag, bedeutet stets, von der Schwere verwirrender Endlichkeit bedrückt zu werden.

Der Ehrgeiz römischer Autoren geht dahin, stets höhere Abstraktionsstufen zu erreichen, die in den Zahlen selbst eingestiftet sind. Zu ihnen gehört auch das Mitzählen des Unsichtbaren, insbesondere der Null.

5. Daß sich die Zahlen 224 und 242 auf den Oktaeder beziehen, ist aus der Analyse der 31 Götterbezeichnungen des CARMEN SAECULARE des Dichters HORAZ ersichtlich gewoden:

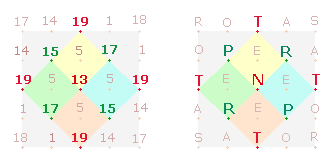
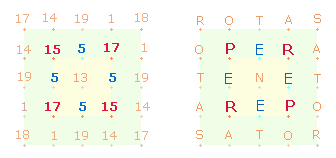
– Die Summe der 3 Werte von zwei Gruppierungen von Götterbezeichnungen (16+18) ist 19*224.

– Die ZS+FS der Initialen des Horaz-Quadrates und des SATOR-Quadrates beträgt 224;

– ebenso die ZS+FS von PARCAE TELLUS, die die zentrische Mitte des HQ bilden.

6. Es handelt sich in diesem Beitrag also, trotz der vorangestellten allgemeinen Einführung, um eine ganz spezielle Untersuchung, auf die von den entprechenden Texten des carmen saeculare verwiesen wird.

II. Bedeutung der Zahlen 224 und 242

1. Im Ausgangsartikel hat sich gezeigt, daß zu zweimal 16 Namen noch 2 hinzufügen sind. Grund hierfür ist, daß eine Oktaederhälfte aus der quadratischen Mittelbasis von 8 Elementen (4 Ecken und 4 Kanten) und 9 Elementen des pyramidalen Aufbaus besteht. Die ungerade Zahl beruht auf die obere Ecke, die durch Zusammenführung der 4 Eckpunkte des DR-Kreuzes entstanden ist. Die untere Ecke der zweiten Oktaederhälfte ist identisch mit dem Mittelpunkt des Tetraktyssterns.

Die Betrachtung des Oktaeders von seiner quadratischen Mittelbasis aus vermittelt eine horizontale Sichtweise des (ganzen) Oktaeders in seinen dreimal 8 Umlaufelementen und der oberen und unteren Ecke. Teilt man ihn in zwei Hälften, besteht jede aus zwei Umläufen und einer Ecke.

In vertikaler Richtung finden sich vier Umläufe von je 8 Elementen, wodurch die 26 Elemente des Oktaeders um 6 überschritten werden. Das Verhältnis von 3:4 Umläufen ergibt 56 Elementen.

2. Betrachtet man – wieder horizontal – die obere und untere Ecke getrennt von den übrigen 3*8 = 24 Elementen, ergeben sich in dreistelliger Zusammensetzung die Zahlen 2-24 und 24-2. Letztere enthält in dem Produkt 2*(11+11) = 22+22 den Vorgang der Oktaederbildung durch ein DR-Kreuz, da eine DR aus 11 Elementen besteht.

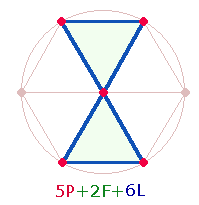
Was in der Einleitung als Konstante von Grundzahlen und Prinzipien durch aufsteigende Ebenen hindurch bezeichnet wurde, zeigt sich in der Kombination von horizontaler und vertikaler Zählung der 8-er Reihen: (3*8 +2) + 4*8 ist 24+2+32 = 56+2 = 58. Da die doppelte Zählung von je 26 Elementen um 6 überschritten wird, kann man auch 52+6 kombinieren. Die Einzelziffern geben eine von drei sanduhrförmigen Doppeldreiecken des Hexagons wieder:

3. Für die gematrische Konzeption des Horaz ist die ZW/FW-Verrechnung der beiden von Bedeutung:

			sm	FW	sm	FW	sm
Z	224	242	466	235
FW	17	24	41	41
sm	3*13*13		507	276	783	38
FW			29	30	59	59
sm					842	97
FW					423	97	520

Von 224 bis 242 sind es 19 Zahlen, ihre Mitte ist 466:2 = 233. Das innerste konzentrische Zahlenpaar sind die Zahlen 234 und 232, die 6 Werte der Götterbezeichnungen TELLUS und CEREREM. Die FW der beiden Zahlen 35 und 21 bilden das Verhältnis 7*(5:3) = 56. 5 Elemente sind es von der unteren zur oberen Ecke, für die zweite Hälfte bleiben 3 übrig.

Auch die Einzelziffern der Zahl 233 ergeben addiert 8. Eine Bedeutung könnte in der Formel 2*(3+3) mit Hinsicht auf die quadratische Mittelbasis liegen: Es handelt sich um 4 Querlinien des DR-Kreuzes, die von je 2 Punkten begrenzt werden. Beim Zusammenfügen des Oktaeders bleiben von den 8 Punkten 4 übrig.

Die Faktoren 3*13*13 der ZS+FS 507 können sich sinnvoll auf die drei quadratischen Rahmen des Oktaeders beziehen, weswegen man durch Drehen jeweils zwei andere untere und obere Ecken bekommt, man also dreimal 13+13 = 26 Elemente des Oktaeders zählen kann.

276 ist die Summe der Zahlen 1-23 und entspricht viermal der ZS 69 für zweimal SATOR ROTAS – Schöpfer, du drehst. Die Einzelziffern 2+3 beziehen sich am ehesten auf 2 Maßeinheiten (Kanten) und 3 begrenzende Punkte (Ecken) von der unteren zur oberen und der oberen zur unteren Ecke. Teilt man 276 in 27+26 auf, kann man darin die 26 Elemente des Oktaeders einmal mit Volumen und einmal ohne sehen.

Die Zahl 59 spielt in der gematrischen Konzeption des Horaz eine besondere Rolle. Ihre Zusammensetzung aus 29+30 weist auf die 15 Rahmenelemente der DR hin, die sich bei der Bildung eines DR-Kreuzes einerseits verdoppeln, andererseits bei Zählung eines einzigen Mittelpunktes auf 29 reduzieren.

4. Die Zahl 233 zeigt sich wiederum, wenn man eine Oktaederhälfte durch die dreistellige Zahl 188 und 881 definiert: Ihre FW sind 51+881 = 932 = 4*233.

5. Die Zahlen 224 bis 242 enthalten 5 Primzahlen: 227+229+223+239+241 = 1169 = 7*167 = FW 174.

Die FW der übrigen Zahlen sind:

Zahl	224	225	226	228	230	231	232	234	235	236	237	238	240	242
FW	17	16	115	26	30	21	35	21	52	63	82	26	16	24	544

Die FS 544 zeigt in der Produktaufteilung= 2*16*17 = FW 27 Ähnlichkeit mit dem Primfaktor 167. Die Erklärung hierfür erfolgt im nächsten Punkt.

Die ZW/FW-Verrechnung der Gesamt-ZS und FS ergibt:

	ZS	FS	sm	FW	sm	FW
	4427	1713	6140	316
FW	252	574	826	68
sm			6966	384	735	29
FW			57	17	74	39
826 = 2*7*59						68

Die Zahlen 17 und 13 der Summe 1713 haben als Gemeinsamkeit, daß sie jeweils eine Hälfte eines Oktaeders darstellen, in ersterem Fall durch Wiederholung der 8 Elemente der Mittelbasis.

Die Summe 6140 faßt zunächst die Numerierung von 1-3 der Kreisachsenelemente zusammen:

Die Produktzahlen 20*307 lassen an die 20 Punkte von zwei Tetraktys denken, von denen eine aus 37 Elementen besteht. Tatsächlich gibt der FW 316 die Aufteilung der 10 Tetraktyspunkte wieder.

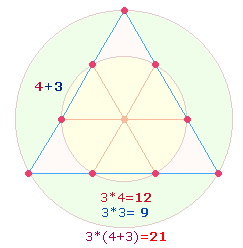
6. Die Konstitutivzahlen für 233 sind 116+117, die – auf dreistelliger Ebene – eine analogische Fortsetzung der Zahlen 16+17 = 33 darstellen. Die Zahlen 16+17 bilden das innere Zahlenpaar für die äußeren Umkehrzahlen 12+21, deren Verhältnis 3*(4:7) zu den Grundpfeilern des Dezimalsystems gehören. Als geometrisches Modell für die beiden Umkehrzahlen ist vor allem der Tetraktysrahmen anzusehen, dessen drei Seiten einzeln gezählt aus aus 3*4 = 12 Punkten besteht und durch 3*3 Linien zur Gesamtsumme von 21 Elementen erhöht werden:

Die Zusammenlegung der ZS+FS beider Zahlenreihen weist auf die Tetraktys als Bezugsmodell. Die FS sind 1713+108 = 1821 = 3*607 = FW 610. Die Aufteilung der Summe 1821 in 18 und 21 zeigt den Doppelaspekt des Tetraktysrahmens: Zählt man die Punkte und Linien des Rahmens nicht je Seite, ist das Ergebnis 18 (9 Punkte + 9 Linien). Der FW 610 enthält diesen Doppelaspekt ebenfalls durch 6+1.

Die ZS beider Reihen sind 4427+165 = 4592 = 16*7 *41 = 112*41 = FW 56. Die FW 610+56 ergeben 666 = 18*37, die, durch die Einzelziffern auf einen Tetraktysrahmen und als Summe der Zahlen 1-36 auf zwei Rahmen beziehbar.

III. Die 2 Zahlenreihen in der Konzeption des Horaz

Es gibt Hinweise darauf, daß Horaz für seine gematrische Konzeption auch die Ergebnisse der beiden Zahlenreihen berücksichtigte.

1. Zur ZS 1800 der 31 Götterbezeichnungen treten einige Verhältnisse mit dem gemeinsamen Faktor 36. Dies zeigt sich besonders in den 3 Werten der 16+16 bzw. 16+18 Bezeichnungen. Die erste Gruppe ist nach ihrer Reihenfolge im Text (R) ermittelt, die zweite durch Ausschlußverfahren (A) gewonnen:

	ZS	FS	VNS	sm
16 N R	858	643	350	1851
16 N A	936	668	664	2268
	1794	1311	1014	4119

Die Summe 1851 = 3*617 zeigt im Faktor 617 eine Umkehrung des Faktors 167 der FS 1169 = 7*167. Letzterer ist auch in 668 = 4*167 enthalten.

Die ZW/FW-Verrechnung der symmetrischen Mitte liefert folgendes Ergebnis:

				sm	FW	sm	FW	sm
Z	233	17	16	266	28
FW	233	17	8	258	48
sm				524	76	600	19
FW				135	23	158	81
sm						758	100	858

Die prime FS 643 könnte sich auf 258 = 6*43 stützen, beziehbar auf 6 Tetraktysseiten mit je 4 Punkten und 3 Linien.

2. Das Endergebnis 858 = 6*11*13 ist insbesondere die Summe der FW der ZS+FS der beiden Zahlenreihen:

	ZS	FS	ZS	FS	sm	FW	sm	FW	sm
	4427	1713	165	108	6413	75	583*11
FW	252	574	19	13	858	29	78*11
sm	7271 = 11*661				7271	104	7375	74	125*59
FW					672	19	691	691
sm	2*109*37 = 111+37 = 37*(3+1)						8066	765	45*17

858 ist auch die Summe 6 Werte des Buchstabenquadrats mit den Wörtern SOL DIVA PARCAE TELLUS CEREREM.

Bemerkenswert ist die Zahl 7271, da 72+71 die Konstitutivzahlen ihrer Summe 143 = 11*13 sind. Die Primzahl 661 enthält in ihren Einzelziffern die Verteilung der 13 Punkte des Tetraktyssterns.

Die Zahl 672, berühmt als "doppelt vollkommen", ist die ZS+FS von 5 von 10 Bezeichnungen, die den Punkten der Tetraktys zugeordnet sind:

	ZS	FS	sm		ZS	FS	sm		ZS	FS	sm
HONOS	67	45	112	GENITALIS	92	76	168	ILITHYIA	88	68	156
				PAX	37	19	56	PUDORQUE	111	69	180
			112				224				336

3. Die Beziehung zur Zahl 233 haben drei Konstellationen:

Erstens, die ZS+FS von TELLUS und CERES:

	ZS	FS	sm
TELLUS	84	63	147
CERES	48	38	86
	132	101	233

Zweitens, die 6 Werte von TELLUS und CEREREM ergeben die doppelte Summe:

	ZS	FS	VN	sm	FW	FW	FW	sm	GS
TELLUS	84	63	29	176	14	13	29	56	232
CEREREM	64	59	30	153	12	59	10	81	234
	148	122	59	329	26	72	39	137	466

Drittens, die ZS von 4 zusammengehörigen Namen ist 233:

SOL	PARCAE	TELLUS	CEREREM		DIVA
43	42	84	64	233	34	267

Für das Buchstabenquadrat kommt noch DIVA hinzu. Die Gesamtsumme 267 kann – wie 276 (s.o.) – ebenso wie 233 als Kennzeichen eines Oktaeders interpretiert werden, wegen des Doppelaspekts von 26 Elementen und 27 Elementen mit Volumen.

IV. Die Zahlen 2 und 3 in Tetraktysstern und Oktaeder

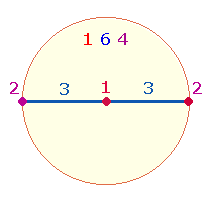
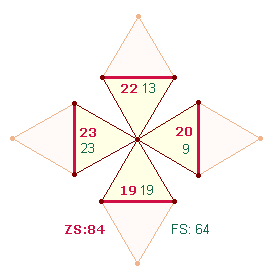
1. Nach der Logik des in der Einleitung Gesagten ist zu erwarten, daß bestimmte Grundzahlen des Tetraktyssterns im Oktaeder auf einer höheren Stufe wiederkehren. Der Radius eines Kreises besteht aus drei Elementen: einer Maßeinheit und zwei Begrenzungspunkten. Bei der Erweiterung zum Tetraktysstern kommen zwei weitere Elemente hinzu. Der Radius ist zweimal zu rechnen, also 2*(3+2). Dabei wird der Mittelpunkt doppelt gezählt:

Im Oktaeder ist der ursprüngliche einzelne Mittelpunkt nicht mehr feststellbar. An seine Stelle treten 6 Ecken. Bei horizontaler Mittelbasis ist eine obere und untere Ecke vorhanden. Dazwischen sind auf jeder Seite jeweils 3 Elemente, entweder Kante-Ecke-Kante oder Fläche-Kante-Fläche. Das ist eine Bedeutung der Zahl 233, wobei 2+3 = 5 Elemente die erste Hälfte und 3 Elemente die zweite Hälfte bezeichnen.

Entsprechend zweier Radien aus jeweils 3+2 Elementen sind auch die Umlaufelemente einer Oktaederhälfte als 2+3 definierbar. Dreht man nun den Oktaeder um 90°, bilden die vorher vertikalen 3 Zwischenelemente die Oberseite und die zwei Ecken befinden sich in horizontaler Position. Dies führt von 2+3 zur Umkehrung 3+2.

2. Das DR-Kreuz, aus dem ein Oktaeder gebildet werden kann, ist auch im SATOR-Quadrat (SQ) in der Gestalt von vier Rautenquadraten vorhanden, denen ein Achsenkreuz mit Mittelpunkt und 4 äußeren Achsenpunkten zugrunde liegt:

Die Summe von je zwei Achsenpunkten berägt 32 (17+15; 19+13). Aus dem Palindromprodukt 2*32 = 64 wird die Umkehrung 3*23 = 69 durch Hinzufügung des Mittelpunkts 5. Während 32+32 in den Ziffern 3+2 den Umlaufelementen von zwei Oktaederhälften zugeordnet werden kann, bezieht sich 3*23 auf je 5 Durchmesserelemente der drei Hexagonachsen. Auffällig ist jedenfalls der Wechsel von 32 zu 23.

3. Die Zahlen 23 und 32 charakterisiert der Gegensatz von Primzahl und 5. Potenz von 2, deren FW 10 ihr eine besondere Bedeutung für das Dezimalsystem verleiht.

Die Eigenschaft 2⁵ setzt 32 in Beziehung zur Doppelraute, die aus 5 hexagonalen und 2 Erweiterungspunkten besteht. Von den 10 Linien der DR verlaufen zwei quer zum Rahmen. Diese beiden Maßeinheiten habe ich unter dem Abschnitt Das Sichtbare und das Unsichtbare als unverfügbar bezeichnet, weil die eine Maßeinheit aus der unsichtbaren Null hervorgeht und die zweite dorthin zurückkehrt. In der 23/24er Numerierung ist die FS der beiden Querlinien einer DR jeweils 32:

Bei der Oktaederbildung werden die 4 Querlinien zur quadratischen Mittelbasis, deren zwei Hälften man durch 3+2 Elemente difinieren kann.

In diesem Sinne kann auch die ZS+FS 1024 = 32*32 des vereinten Horazquadrats und des SQ verstanden werden.

4. Die gleiche FS 32 ist aus zweimal der ZS 42 entstanden (s. Grafik). Dasselbe Ergebnis kommt jedoch auch zustande durch die Addition der FS 32 und ihrem FW 10. Aus diesem Grund können im SQ die 4 Mittelpunkt-E aus der ZS 42 und der FS 32 erklärt werden:

Wenn man auch von der ZS 42 den FW 12 bildet, zeigt sich, daß sich die FS 32 auf 96 verdreifacht:

ZS	FW	sm	FS	FW	sm	GS
42	12	54	32	10	42	96

Das Gesamtergebnis ist für zweite Doppelraute auf 192 zu verdoppeln.

Die Zahl 32 wurde eingangs bereits erwähnt als 4 Umläufe von je 5 Elementen vom unteren zum oberen Eck und weiteren 3 Elementen. Diesen Vorgang kann man mit den übrigen vier Ecken zweimal wiederholen und kommt so auf die Zahl 96.

5. Die Umkehrzahlen 23+32 = 55 ergeben die Summe der Zahlen 1-10. Ihre FW seien zum Schluß aufgeführt, um noch einmal das Prinzip gleicher Grundzahlen auf verschiedenen Ebenen zu zeigen:

ZW	23	32	55
FW	23	10	33
33:55 = 11*(3:5)

Eine erste Beziehung gibt es auf der Ebene der Kreisachse zwischen 3 Radialelementen als Grundeinheit und 5 Durchmesserelementen.

Auf der Ebene des Tetraktyssterns und der beiden konzentrischen Kreise bedeuten 3:5 Radialelemente das Flächenverhältnis 1:3.

Auf der Ebene des Oktaeders ist das Ineinander von Elementen aufgehoben. Hier bezeichnen 5:3 Elemente zwei Hälften eines Umlaufs, da die untere und obere Ecke je 2 Kanten trennt.

Auf dreistelliger Ebene heißen die Zahlen, die zwei Hälften und das Ganze eines Oktaeder bezeichnen, 558, 585, 855:

	Zahl	Fkt.	FW
Zahl	558	18*31	39
FW	585	45*13	24
	855	45*19	30
sm	1198		93

Der FW 39 = 3*13 und die Gesamt-FS 93 = 31*3 mag ein Hinweis darauf sein, daß ein Oktaeder aus zwei Doppelrauten hervorgeht, deren Punktemuster 3:1:3 ist:

Erstellt: August/September 2011

Start

Inhalt