64 Zweistellige
Komplementärzahlen
V. 64 Komplementärzahlen auf 49 Quadratpunkten
VI. 64 Komplementärzahlen im 9x9
Punkte-Quadrat
V. 64 Komplementärzahlen auf 49
Quadratpunkten
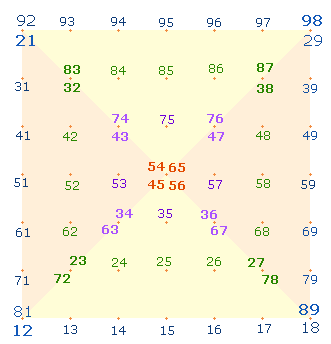
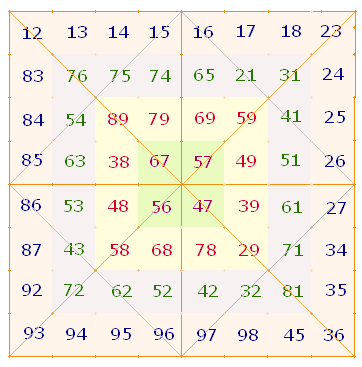
1. Die 64 Komplementärzahlen lassen sich auf 49 Punkten dreier konzentrischer Quadrate eintragen:
|
|
Die äußere Zahlenreihe ab 12 beginnt – in Anlehnung an das SATOR-Quadrat – unten links. Die Komplementärzahl 98 ist diagonal auf dem obersten rechten Punkt gesetzt, die Umkehrung 21 auf dem obersten linken Punkt und die Komplementärzahl 89 auf dem untersten linken Punkt. Diese Anordnung erscheint die befriedigenste Lösung.
Die Anordnung in drei konzentrischen Quadraten ist möglich, da die 16 Basiszahlen (BZ) der 64 Komplementärzahlen sich über vier Zehnereinheiten in der Häufigkeit 7+5+3+1 erstrecken. Anfangs- und Endzahl der ersten drei Reihen besetzen jeweils die Eckpunkte, so daß sich in der Mitte jedes Quadratviertels 5+3+1 Zahlen befinden. Jedes Quadratviertel besteht demnach aus 7 Diagonal- und 9 Binnenzahlen. Die Zahlensumme (ZS) von je 4 Komplementärzahlen beträgt 220, somit für die beiden Diagonalen 1540 und die Binnenbereiche 1980, zusammen 3520 = 16*220.
Die Einerstellen jeder Reihe ergänzen sich konzentrisch jeweils zu 10.
Die Mittelreihe des Quadrats besteht aus 10, die übrigen sechs aus je 9 Zahlen.
Zu den ZS sind noch die Faktorensummen (FS) hinzuzunehmen:
|
|
2. Die ZS+FS der 64 Komplementärzahlen ist 3520+1750 = 5270 = 10*17*31.
Die Anfangszahlen betreffen alle vier Zahlenreihen, die Endzahlen nur die Reihen von 1-3. Die FS der Anfangs- und Endzahlen sind:
|
|
A |
E |
sm |
|
A |
E |
sm |
GS |
|
BZ |
60 |
27 |
87 |
KZ |
89 |
149 |
238 |
325 |
|
UK |
74 |
37 |
111 |
KZ |
187 |
97 |
284 |
395 |
|
|
134 |
64 |
198 |
|
276 |
246 |
522 |
720 |
|
A: 134+276 = 410; E: 64+246 = 310 |
||||||||
|
198:522 = 18*(11:29) |
||||||||
|
238 = 14*17; 284 = 4*71 |
||||||||
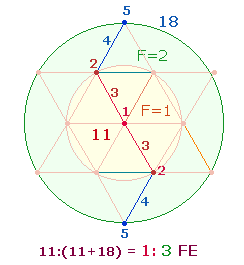
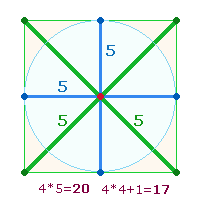
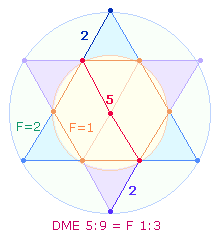
Die Verhältniszahlen 11:29 stellen Numerierungssummen von 5 und 9 Durchmesserelementen dar und geben das Kreisflächenverhältnis 1:3 wieder:
|
|
3. Die FS der vier Zahlenreihen auf den Diagonalen (Di) und im Binnenbereich (Bi) sind:
|
10-St. |
1 |
2 |
3 |
4 |
|
|
Di. |
198 |
208 |
261 |
53 |
720 |
|
Bi. |
690 |
240 |
100 |
– |
1030 |
|
|
888 |
448 |
361 |
53 |
1750 |
|
208+53 = 261;
208:240 = 16*(13:15) |
|||||
|
448:1302 = 14*(32:93) |
|||||
Die FS 198 der ersten Zahlenreihe bewirkt zum zweiten Mal das Verhältnis 18*(11:29) zur restlichen Summe. Durch die Addition der FS der zweiten und vierten Zahlenreihe ergibt sich für die Diagonalwerte zweimal 261 = 9*29: Numeriert man die 9 Durchmesserelemente der Doppelraute (DR) von der Mitte aus von 1-5, ergibt sich die Summe 29.
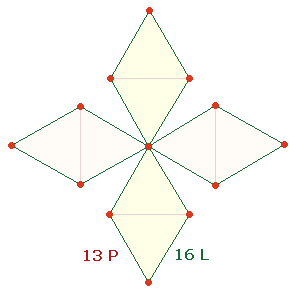
Die drei FS 208, 261 und 53 sind auf den Oktaeder bezogen: Die Faktoren 13*16 = 208 weisen auf 29 Rahmenelemente des DR-Kreuzes (zur Bildung des Oktaeders), das aus 13 Punkten und 16 Linien besteht:
|
|
Die Zahl 261 kann als 26+(26+1) = 53 gelesen werden und bedeutet den Doppelaspekt von 26 äußeren Elementen des Oktaeders, beim zweiten Mal 27 Elemente unter Einschluß des Volumens.
Die drei FS 690, 240 und 100 des Binnenbereichs sind jeweils durch 10 teilbar. Die Additionen der ersten und zweiten Summe sowie der zweiten und dritten Summe weisen auf die Teilbarkeit der ZS+FS 5270 = 10*31*17 hin: 690+240 = 930 = 30*31, 240+100 = 340 = 20*17.
Durch zwei weitere Additionen der Diagonalwerte ist die Teilbarkeit durch 7 der FS 1750 berücksichtigt: 198+208 = 406 = 14*29, 208+261 = 469 = 7*67. Beide Summen ergeben die Hälfte von 1750.
4. Die ZS+FS der Diagonalzahlen ergibt 1540+720 = 2260 = 20*113. Die Teilbarkeit durch 9 der ZS 1980 der Binnenzahlen bewirkt die Umkehrung der FS 1030: 1980+1030 = 3010.
5. Die ZS+FS der vier Zahlenreihen sind:
|
10-St. |
1 |
2 |
3 |
4 |
|
|
ZS |
1540 |
1100 |
660 |
220 |
3520 |
|
FS |
880 |
448 |
361 |
53 |
1750 |
|
|
2428 |
1548 |
1021 |
273 |
5270 |
|
2428 = 4*607 |
|||||
|
1548+273 = 1821 = 3*607 |
|||||
Auffällig ist der zweimalige Primzahlfaktor 607. Sie kann sich auf die Elemente der 3 Tetraktysseiten mit der Doppelzählung 3*6 (alle zusammen) und 3*7 (jede einzelne Seite) beziehen und auf je 13 Elemente von 4 Doppeldreiecken, aus denen der Oktaeder besteht.
Die Primzahl 1021 kann als Zusammensetzung des FW 10 der Zahl 21 betrachtet werden. Die Einzelziffern geben das Kreisflächenverhältnis 3:1 der beiden Tetraktyskreise wieder.
Durch konzentrische Addition ergibt sich: 2428+273 = 2701 = 37*73 >110; 1548+1021 = 2569 = 7*367 >374. Die Einzelziffern der Umkehrfaktoren 37 und 73 sind auf die jeweils 10 Punkte von zwei Tetraktys zu beziehen, die des Faktors 367 wiederum auf den Doppelaspekt der Elemente der drei Tetraktysseiten. Die FW 110 und 374 bilden das Verhältnis 22*(5:17) = 22*22. Das Produkt 37*73 zeigt die enge Beziehung zwischen Kreis, besonders den Tetraktyskreisen, zum Quadrat.
6. Die horizontalen und vertikalen Summen können der Relevanz und inneren Begründung der festgelegten Anordnung herangezogen werden, liegen jedoch nicht so auf der Hand, daß sich eine Behandlung lohnte. E i n e Berechnung erscheint jedoch von Interesse. Die unterste und oberste Zeile haben folgende ZS+FS:
|
|
ZS |
FS |
|
||||
|
|
7 Za. |
2 Za. |
sm |
7 Z. |
2 Z. |
sm |
GS |
|
u. Ze. |
105 |
170 |
275 |
70 |
101 |
171 |
446 |
|
o. Ze. |
665 |
50 |
715 |
260 |
39 |
299 |
1014 |
|
|
770 |
220 |
990 |
330 |
140 |
470 |
1460 |
|
330:770 = 110*(3:7); 140:220 = 20*(7:11) |
|||||||
|
275:715 = 55*(5:13); 470:990 = 10*(47:99) |
|||||||
|
299:715 =
13*(23:55); 1460 = 20*73 |
|||||||
Auffällig sind mehrere Zahlenverhältnisse. Durch 11 teilbar sind auch FS und ZS der linken und rechten Vertikalseite, die aus je 5 verbliebenen Zahlen bestehen:
|
|
li. |
re. |
sm |
|
ZS |
255 |
295 |
550 |
|
FS |
224 |
194 |
418 |
|
|
479 |
489 |
968 |
|
418:550 = 22*(19:25) = 22*44 |
|||
|
255:295 = 5*(51:59) |
|||
Addiert man zu 968 die ZS+FS 273 der Mittelpunktszahlen, ergibt sich das Verhältnis von 14:18 Komplementärzahlen und dem ZS+FS-Verhältnis 1241:1460 = 73*(17:20). Das Verhältnis 17:20 ist aus zweierlei Gründen von Bedeutung:
Erstens, die horizontale und vertikalen Achse sowie zwei Diagonalachsen des kleinsten Quadrats bestehen – vergleichbar mit der Kreisachse – aus je 5 Elementen, zusammen 20. Rechnet man nur einen Mittelpunkt, entfallen 3 Elemente:
|
|
Zweitens, die ZS+FS der Zahlen 1-9 und 1-10 sind 45+55 = 100 und 39+46 = 85, woraus sich das Verhältnis 5*(20:17) ergibt.
VI. 64
Komplementärzahlen in 64 Quadraten
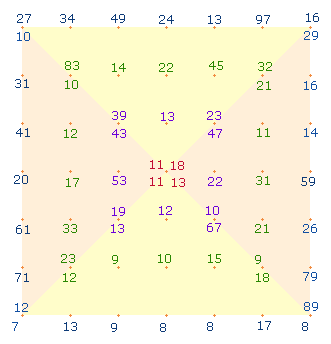
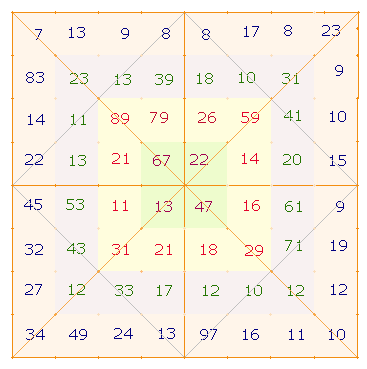
1. Die innere Ordnung der 64 Komplementärzahlen zeigt sich ebenfalls eindrucksvoll, wenn man sie in ebensoviele Einzelquadrate eine 9x9 Punktequadrats anordnet, links die Zahlenwerte (ZW), rechts die Faktorenwerte (FW):
|
|
|
Die 64 Zahlen werden von außen nach innen in 4 konzentrische Quadratrahmen eingetragen. Oben links beginnen die 16 Basiszahlen, es folgen die komplementären Entsprechungen, es folgen die Umkehrungen der Basiszahlen und der komplementären Entsprechungen.
Worin die innere Ordnung besteht, soll besonders an den ZS+FS der Zahlen auf den großen und kleinen Diagonalen gezeigt werden.
2. Für die oberen und unteren Diagonalhälften ergeben sich folgende Werte:
|
12 |
76 |
89 |
67 |
244 |
57 |
59 |
31 |
23 |
170 |
414 |
|
7 |
23 |
89 |
67 |
186 |
22 |
59 |
31 |
23 |
135 |
321 |
|
|
|
|
|
430 |
|
|
|
|
305 |
735 |
|
93 |
72 |
58 |
56 |
279 |
47 |
29 |
81 |
36 |
193 |
472 |
|
34 |
12 |
31 |
13 |
90 |
47 |
29 |
12 |
10 |
98 |
188 |
|
|
|
|
|
369 |
|
|
|
|
291 |
660 |
|
735:660 = 15*(49:44) = 1395 = 45*31 |
||||||||||
Die ZS+FS der 16 Diagonalzahlen zu den 48 übrigen Zahlen bilden das Verhältnis 5*31*(9:25). Die Verhältniszahlen 9 und 25 stellen zwei konzentrische Quadrate aus 9 und 25 Punkten dar.
Die Summen 186+279 = 3*31*(2+3) = 93*5 bilden ein Drittel der Gesamtsumme 1395. Das Verhältnis der FS 186+90 = 276 zu den ZS 244+170 = 414 beträgt 6*23*(2:3) = 690. Je vier Summen haben das ZS+FS-Verhältnis 690:705 = 15*(46:47).
Je 8 Diagonalzahlen befinden sich innerhalb und außerhalb des Rautenquadrats:
|
|
in. |
au. |
|
|
ZS |
462 |
424 |
886 |
|
FS |
357 |
152 |
509 |
|
|
819 |
576 |
1395 |
|
357:462 = 21*(17:22) |
|||
|
819 = 63*13; 1395 = 45*31 |
|||
Die ZS+FS 576 = 24² bewirkt, als Teil zum Ganzen, die
Umkehrung des Faktors 13
zu 31. Der
durchschnittliche ZW+FW der 8
äußeren Diagonalzahlen ist 72. Die FW der Summen 819
und 1395 sind 26
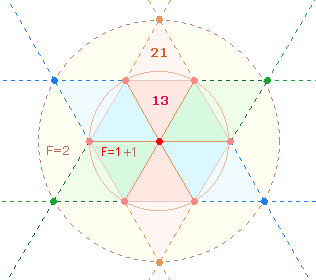
und 42. Ihr Verhältnis 2*(13:21) bedeutet, auf die Doppelraute (DR) des Hexagramms und seine zwei
konzentrischen Kreise bezogen, das Kreisflächenverhältnis 1:3. Denn die 13
Elemente des hexagonalen Bereichs vertreten die Flächeneinheit 1 des hexagonalen Kreises und
die 21 Elemente der ganzen DR die Flächengröße 3:
|
|
Die Zahlen 13 und 21 sind auch als Faktoren in der ZS+FS 819 = 3*13*21.
3. Die 64 Zahlen können in vier Quadrate zu je 16 Zahlen aufgeteilt werden. In der folgenden Tabelle stehen jeweils an erster Stelle die ZS und FS der Diagonale von oben links nach unten rechts. Zur Hälfte sind sie bereits bekannt (grün unterlegt):
|
244 |
229 |
473 |
104 |
170 |
274 |
747 |
|
186 |
54 |
240 |
74 |
135 |
209 |
449 |
|
430 |
283 |
713 |
178 |
305 |
483 |
1196 |
|
287 |
279 |
566 |
193 |
227 |
420 |
986 |
|
134 |
90 |
224 |
98 |
187 |
285 |
509 |
|
421 |
369 |
790 |
291 |
414 |
705 |
1495 |
|
851 |
652 |
1503 |
469 |
719 |
1188 |
2691 |
|
1196:1495 = 13*23*(4:5); 713:483
= 23*(31:21) |
||||||
|
1503:1188 = 9*(167:132) |
||||||
|
851
= 37*23; 414 = 18*23 |
||||||
|
240:224 = 16*(15:14); 209:285 = 19*(11:15) |
||||||
Die Ergebnisse sind hauptsächlich auf die Zahlen 9 und 23 ausgerichtet. Die acht Diagonalen sind den Doppelrauten (DR) des Tetraktyssterns vergleichbar:
|
|
Dem
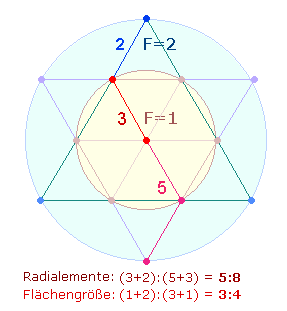
oben ermittelten Verhältnis 4:5 entsprechen die 9 Durchmesserelemente der DR: 5 hexagonale Elemente stehen für
eine 1 Flächeneinheit, 4
Erweiterungselemente für 2
Flächeneinheiten, 5:9 Durchmesserelemente geben das Verhältnis 1:3 wieder.
Die Addition der DM-Elemente ergibt 9+14 = 23. Die beiden Kreisflächenverhältnisse werden in dem oben ermittelten Verhältnis 31:21 in zweistelliger Umkehrung wiedergegeben.
Der Faktor 13 ist auf die entsprechenden Radialelemente zu beziehen:
|
|
Als dreistellige Zahl 149 erscheint 14+9, wenn man die inneren 4 Zahlen der Diagonalen addiert:
|
294 |
152 |
446 |
136 |
141 |
277 |
723 |
|
235 |
213 |
448 |
119 |
122 |
241 |
689 |
|
|
|
894 |
255 |
263 |
518 |
1412 |
|
894 = 6*149; 518 =
14*37; 1412 = 4*353 |
||||||
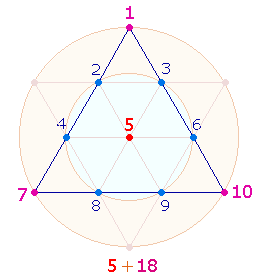
Die FS 518 ist insbesondere auf die numerierten Tetraktyspunkte zu beziehen, indem den Mittelpunkt die Zahl 5 besetzt und 18 die Summe der Eckpunkte bildet:
|
|
Die Gesamtsumme 1412 weist auf die 14+12 Elemente des Oktaeders hin.
4. Schließlich kann man die ZS+FS aller vier Quadrate ermitteln:
|
oben |
unten |
|
||
|
921 |
592 |
1155 |
852 |
3520 |
|
511 |
331 |
458 |
450 |
1750 |
|
1432 |
923 |
1613 |
1302 |
5270 |
|
1302 = 2*21*31
= 42*31 |
||||
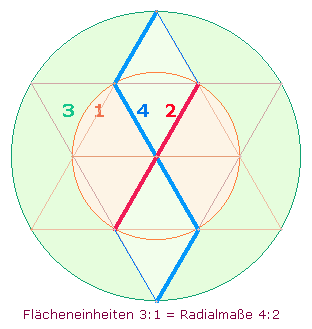
Die untere rechte Summe 1302 stellt in ihrer Teilbarkeit durch 31 die größte Annäherung an ein Viertel der Gesamtsumme 170*31 dar. Die Faktoren 21 und 31 geben erneut die beiden trinitarischen Kreisflächenverhältnisse wieder. Die Produktdarstellung 42*31 enthält die ersten vier Zahlen. Bezieht man die Einzelziffern 4 und 2 auf die Radialmaße des DR-Durchmessers, repräsentieren sie das Kreisflächenverhältnis 3:1:
|
|
Fügt man zu 1302 die Diagonalwerte 713 des oberen rechten Quadrats (s.o.) hinzu, erhält man 2015 und das Verhältnis 5*31*(13:21) = 155*34 zur übrigen Summe. Wiederum sind in den Einzelziffern die beiden Kreisflächenverhältnisse zu erkennen. In Bezug auf die 21 Elemente der DR geben die beiden Verhältniszahlen das Kreisflächenverhältnis 1:3 wieder, insofern der hexagonale Bereich aus 13 Elementen besteht.
5. Das innere Rautenquadrat – dessen äußerer Rahmen die in den Kästchen enthaltenen Zahlen einschließen – kann als zwei Doppelrauten und somit in Bezug zu den DR des Tetraktyssterns gesehen werden. Die Analogie zeigt sich in der ZS 2238 = 6*373 von 40 Zahlen. Die Einzelziffern der Primzahl 373 zeigen die Aufteilung der 13 Punkte des Tetraktyssterns. Die Einzelziffern der Zahl 2238 geben die 15 Elemente des DR-Rahmens wieder: 2+2 Querpunkte, 3 Achsenpunkte und 8 Linien.
64 Komplementärzahlen auf Würfeln und Oktaedern
Erstellt: November 2014