Grundelemente
des Dezimalsystems
Dieser Beitrag ist parallel zu dem Ausgangsartikel Entwicklung des Dezimalsystems zu verstehen. Der
trinitarische Aspekt bleibt hier im Hintergrund. Schwerpunkt dieser Arbeit sind
die Achsen 1-3.
Die beiden Kreise sehe ich jetzt als Doppelkreis des Tetraktyssterns.
Darüber ein neuerer Beitrag vom Januar 2007 Die trinitarische
Gleichung 1+2=3.
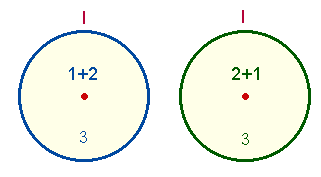
1. Am Anfang von allem steht die Gleichheit zweier Kreise. Denn der Kreis hat 3 Bestandteile: Mittelpunkt (MP), Kreislinien und Fläche (F). Der Zahl 3 gehen jedoch 1 und 2 voraus, die zusammen 3 ergeben.
Setzt
man die Zahlenfolge 1+2+3 bis zu ihrem Additionsergebnis 6 fort, entsteht
wiederum ein 1:1-Verhältnis: 1+2+3 || 4+5+6. Konzentrisch einander zugeordnet sind 1+6,
2+5, 3+4, zusammen 3*7 = 21, was zur
Umkehrung der ersten beiden Zahlen 12
führt. Die ersten beiden konzentrischen Zahlenpaare bilden in ihrer Umkehrung
die Zahlenwerte der Zeilen 2-4 des SATOR-Quadrats: 52-61-52.
|
|
Ausdruck der Gleichheit ist zweimal die Zahl 1, nebeneinander gestellt 11, nach dem römischen Zahlsystem I I, zweimal der Buchstabe I. Da das I der 9. Buchstabe ist, bedeutet dies 9 Punkte (P) und 9 Linien (L) im Tetraktysrahmen.
Zweiheit als kleinstes Zahlensymbol der Vielheit bedeutet in der Form zweier identischer Kreise Einheit des kosmischen Räderwerks.
1 ACHSE
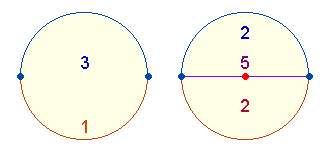
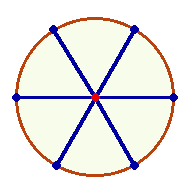
2. Das Grundmotiv der Gleichheit setzt sich im Einzelkreis selbst fort durch Erzeugung zweier Hälften von Kreislinie, Durchmesserlinie (DM) und Fläche.
3. Jede Halbierung erfordert Trennungsmarkierungen, die als zählbare Größe zum Sinngefüge des Zahlsystems gehören. Wenn nun eine Kreislinie durch zwei Punkte halbiert ist, sind diese als Trennungsmarkierungen einer der beiden Hälften zuzuordnen, und die 4 Elemente des Kreisbogens teilen sich auf im Verhältnis 3:1. Da aber jede Hälfte 3 Elemente beanspruchen kann, gibt es auch das Verhältnis 3:3. Dieser Doppelaspekt führt durch (3+1)+(3+3) erstmals zur Zahl 10. Wenn man Mittelpunkt und Fläche noch zweimal hinzurechnet, erhält man (4+2)+(6+2) = 6+8 oder 10+4. Die beiden letzteren Zahlen gehören zusammen, da die fortlaufend Addierung der Zahlen von 1 bis 4 die Zahl 10 ergibt.
|
|
Eine formale Gleichheit von 2+2+2 wird erreicht, wenn 2 Punkte, 2 Halbbogen sowie Mittelpunkt und Fläche als Einheiten gruppiert werden.
4. Zieht man durch den MP eine Durchmesserlinie, ergeben sich sich zwei Halbierungen: der Fläche und des Durchmessers. Wiederum ist dem Doppelaspekt der Halbierung durch Doppelzählung Rechnung zu tragen: Eine Kreisflächenhälfte besteht nun aus halbem Kreisbogen, halber Kreisfläche und den 5 Begrenzungselementen des Durchmessers. Das Aufteilungsverhältnis für den ganzen Kreis lautet somit 2:5:2 = 9. Eine Hälfte verhält sich zur zweiten 7:2. Nimmt man für jede Hälfte 7 Elemente in Anspruch, erhält man (7+2)+(7+7) = 23.
In analoger Weise lautet die Rechnung für die Durchmesserelemente (3+2)+(3+3) = 11. Der Doppelaspekt der DM-Elemente führt wieder zur Gleichheit von 1:1.
Für die Aufteilung der Zahl 11 kommen 3 Verhältnisse in Frage:
1. 5+6: DM-Elemente + 2*3 Radialelemente
2. 4+7: 2*2 Linien + 2*2 Außenpunkte und 3 MP
3. 3+8: 3 MP + 2*2 L + 2*2 P.
Die konzentrische Mitte der drei Aufteilungen bildet 4+7.
Bezieht man in die Doppelzählung der 5 DM-Elemente auch die 4 übrigen Kreiselemente mit ein, erhält man 9+10 bzw. 11+8 = 19 als Gesamtergebnis.
5. Zum Ergebnis eines Prozesses kann man auch davor liegende Schritte hinzuzählen. Den 5 DM-Elementen geht der MP des "Rohkreises" vorher. Somit ist der Ausgangspunkt der Gleichung 1+2 = 3 erreicht: 1 für den MP, 2 für die Radiallinien, 3 für die Begrenzungspunkte.
2 ACHSEN
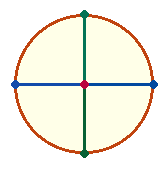
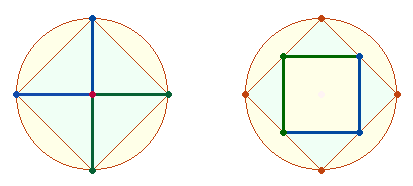
6. Wenn der Kreisdurchmesser eine neue kategoriale Größe darstellt, bedarf er der Entfaltung durch eine Zweiheit und Dreiheit. Dies geschieht durch Hinzufügung von einer und zwei weiteren DM-Linien: 1 + (1+1) + (1+2). Legt man eine zweite DM-Linie im rechten Winkel durch den MP, wird die Kreisfläche ein weiteres Mal geteilt und es entstehen 4*4 gleiche Elemente + MP = 17.
|
|
|
Das neugeschaffene Achsenkreuz besteht bei einem gemeinsamen MP aus 9 Elementen. Um nun sowohl den DM-Elementen als auch den Radialelementen Rechnung zu tragen, verfährt man auf zweifache Weise:
a) Man zählt zu den 9 Achsenkreuzelementen 2*5 DM-Elemente hinzu und erhält das Ergebnis 19.
b) Man beläßt für eine Achse den Mittelpunkt und fügt für die 2. Achse 2 MP hinzu. Die Doppelrechnung löautet dann 9+11 = 20. Durch Addition beider Ergebnisse (19+20) erhält man 39.
Nimmt man zum Achsenkreuz noch die übrigen 8 Elemente hinzu, ergibt sich 9+8 = 17, 10+8 =18, 11+8 = 19. Verbindet man die erweiterte Zählung mit der Ausgangszählung, erhält man 17+18=35, 17+19=36; 35+36=71. Die der alphabetischen Ordnung entsprechenden Buchstaben sind RST, die im Wort SATOR vorkommen.
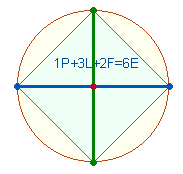
Durch Hinzukommen einer zweiten Achse wird erstmals die Konstruktion eines Dreiecks möglich, indem von zwei Endpunkten einer Achse je eine Verbindungslinie zum Endpunkt der zweiten Achse hergesteltt wird. Verfährt man ebenso mit dem gegenüberliegenden Punkt, entsteht ein Quadrat mit dem Flächeninhalt 2.
Die Eigenschaft des so erzeugten Quadrats besteht darin, daß die 4 Schnittpunkte ebenso wie die sich schneidenden Achsen selbst im rechten Winkel liegen.
Löst man einen Winkel vom Mittelpunkt des Achsenkreuzes, kann man ihn so verschieben, daß die beiden Endpunkte an den Enden des anderen Winkels anliegen und ein Quadrat von der Größe 1 bilden. Dieses kleine Quadrat kann man an den Schnittpunkten der Seitenhalbierenden in das Rautenquadrat einfügen. Das so gewonnene Doppelquadrat ist nun ohne Konstruktionsmittelpunkt und besteht aus 25 Elementen. Das in der Mitte befindliche Quadrat ist Grundeinheit rationaler Fächenberechnung und kann sich mit anderen Quadraten nahtlos zusammenschließen.
|
|
3 ACHSEN
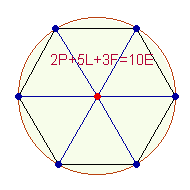
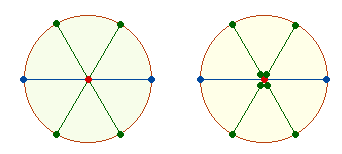
7. Ein Achsenkreuz aus drei Achsen hat wiederum die Absicht, gleiche Teile zu schaffen. Die Achsen stehen im 60° Winkel zueinander und die Kreislinienpunkte haben Radiusabstand voneinander. Verbindet man sie, entstehen 6 gleichseitige Dreiecke, als ganze Figur Hexagon genannt. Diese Figur vereinigt die Dreiheit der Achsen mit der Zweiheit der Radien. Je eine Kreishälfte enthält drei Dreiecke. Die Grundaddition 1+2+3=6 erscheint somit als 2*3 Dreiecke, aber auch als 3*2 Dreicke, weil jedes Dreieck sich in spiegelgleicher Umkehrung in der 2. Kreishälfte fortsetzt.
|
|
|
8. Das Hexagon enthält also eine Reihe idealer Verhältnisse. Der Winkel zweier Segmentlinien ist jedoch nicht mehr identisch mit der Winkel zwischen zwei Achsen, sondern doppelt so groß. Die Flächenberechnung ist nicht so rational wie beim Quadrat und die Außenseite des Hexagon läßt keinen nahtlosen Anschluß zu.
Ein Vergleich beider Achsenkreuze läßt den Schluß zu, daß sie sich komplementär ergänzen. Sie können als konstitutive Form für die Zahl 10 angesehen werden, da sich einerseits 4+6 Radiallinien gegenüberstehen und sich andererseits die Zahle 2+3 =5 Achsen durch je zwei Radien verdoppelt.
Die Addition der DM-Elemente beider Achsenkreuze ergibt weiterhin den Wert 5*5 = 25, so daß das SATOR Quadrat mit seinen 25 Buchstaben als Zusammenführung beider Achsenfiguren aufzufassen sind.
9. Die dreifache Zählweise der
Durchmesserelemente führt zu den Zahlen 13, 15 und 17, bzw. 13+15 = 28, 17+13 =
30; 30+28 = 58. Die Zahl 58 hat eine besondere Beziehung zum Oktaeder mit
seinen 8 Umlaufelementen und 5 Elementen für eine Hälfte. Die folgende Tabelle
gibt eine Übersicht über die Zahlenverhältnisse:
|
Achsen |
Sym-El
+ 1MP |
Radial-El + x MP |
Sum. |
DM-El
alle. |
Sym-El
+ 1MP |
Sum. |
Gs.Sum. |
|
1 |
5 |
6 |
11 |
– |
– |
– |
11 |
|
2 |
9 |
11 |
20 |
10 |
9 |
19 |
39 |
|
1+2 |
14 |
17 |
31 |
10 |
9 |
19 |
50 |
|
3 |
13 |
17 |
30 |
15 |
13 |
28 |
58 |
|
1+2+3 |
27 |
34 |
61 |
25 |
22 |
47 |
108 |
Für den einfachen Durchmesser sind 2 Radialelemente dadurch darstellbar,
daß man eine zweite Achse im rechten Winkel hinzusetzt und mit zwei MP
versieht. Eine solche Darstellung entspricht gleichzeitig der zweiten Zählung
des zweiachsigen Kreuzes.
Dagegen ist die doppelte Zählung der DM-Elemente nicht darstellbar,
da die Symmetrie nur einen Mittelpunkt duldet und ein zweiter MP nicht allein
stehen kann; diese Zählung kann also nur gedacht werden.
Die erste und zweite
Zählung der Radialelemente ergibt für das zweiachsige Achsenkreuz das MP-Verhältnis
1:3, für das dreiachsige 1:5, zusammen 2:8. Die Doppelzählung von DM-Elementen
und Radialelementen führt bei den zwei Achsenkreuzen zur doppelten Zahl der
Radialelemente, beim einfachen DM zu einer ungeraden Zahl.
|
|
|
Rechnet man die DM-Elemente mit einem Mittelpunkt nur einmal und unterscheidet zwischen den je gegenüberliegenden Symmetrieelementen und der Zahl der Mittelpunkte, ergeben sich folgende Zahlenverhältnisse:
|
|
Sym-El
+1MP |
|
Alle
DM-El |
|
Radial-El |
|
|
|
Achsen |
Sym-El
|
MP |
Sym-El |
MP |
Sym-El |
MP |
Gs.Sum. |
|
1 |
4 |
1 |
– |
– |
4 |
2 |
11 |
|
2 |
8 |
1 |
8 |
2 |
8 |
3 |
30 |
|
3 |
12 |
1 |
12 |
3 |
12 |
5 |
45 |
|
1+2+3 |
24 |
3 |
20 |
5 |
24 |
10 |
86 |
|
|
|
|
|
|
|
|
|
|
Sym-El |
24+20+24 = 68 |
||||||
|
MP |
3+5+10 = 18 |
||||||
|
Ges. |
68+18=86 |
||||||
Die Trennung der Symmetrieelemente von den Mittelpunkten zeigt ein Umkehrergebnis, indem die 68 Symmetrieelemente durch Hinzufügung der 18 MP zur Umkehrzahl 86 führen. Die Zahlen 8+6 sind konstitutiv für die Zahl 14, den ZW für das O. Sie beziehen sich insbesondere auf die 6 Punkte und 8 Linien der an den Enden zusammengefügten Doppelraute. Zieht man die 8+3 Elemente des einzelnen DM ab, beträgt das Verhältnis der Symmetrieelemente zu den Mittelpunkten 60:15 = 15*(4+1). Die drei Zählungen der beiden Achsen ergeben, wie aus der Tabelle ersichtlich, jeweils das Dreifache des Mittelwertes: 3*(10+15). (Der Mittelwert bezeichnet die volle Zahl der Durchmesserelemente.)
10. Da das Achsenkreuz eine eigene Kategorie des Zahlsystems darstellt, bilden der 2-achsige und der 3-achsige Kreis eine Einheit, sie führen aber Grundkategorien der einachsigen Kreisfigur weiter. Die beiden Achsenkreuze ermöglichen die Konstruktion von Quadrat und Dreiecken. Die Segmentlinien übernehmen dabei die Sektorenbögen und die so definierten Flächen die Sektoren. Das Rautenquadrat und das Hexagon machen sich gewissermaßen vom Kreis unabhängig. Dadurch aber gewinnt der Kreis seine Eigenberechtigung zurück und steuert seine 3 Elemente noch hinzu. Für die beiden Achsenkreuze lauten also die Zahlen 17+3 = 20 und 25+3 = 28. Das Verhältnis beider Ergebnisse ist 4*(5+7) = 48.
11. Die Doppelzählung der Elemente zweier Kreishälften erbringt folgende Werte:
|
Achsen |
1.Hälfte m. DM-E |
2.Hälfte o. DM-E |
1.+2. Hälfte m. DM-E |
Summe |
Elemente ganzer Kreis |
|
1 |
7 |
2 |
14 |
23 |
9 |
|
2 |
11 |
6 |
22 |
39 |
17 |
|
1+2 |
18 |
8 |
36 |
62 |
26 |
|
3 |
15 |
10 |
30 |
55 |
25 |
|
1+2+3 |
33 |
18 |
66 |
117 |
51 |
|
Halbbögen |
3 |
1 |
6 |
10 |
4 |
|
|
36 |
19 |
72 |
127 |
55 |
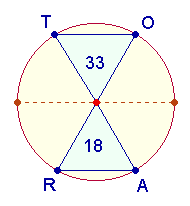
Die Zahl 51 für die Gesamtheit der Kreiselemente ist auch der Zahlenwert für ROTA. Dabei übernimmt OT mit 14+19 = 33 die 1. Hälfte und RA mit 17+1 die zweite Hälfte. Darstellbar ist dieses Verhältnis durch die 4 Kreislinienpunkte des mittleren Doppeldreiecks des Hexagons.
|
|
12. Die 2*(2+3) = 10 Radiallinien sind eine wesentliche Grundlage für das Dezimalsystem. Doch die zusätzlichen 2 Radiallinien des einachsigen Kreises räumen auch der 12 eine wichtige Rolle ein, besonders in der Zeitrechnung. Dazu gehören vor allem die 2*12 Stunden des Tages und die 12 Monate des Jahres. Die Zahl 10 läßt nur die Teilung durch 2, die Zahl 12 außerdem die Teilung durch 3 und 4 zu.
Bildet man die Zahlen- und Faktorensumme der Zahlen 1-9 (2 Achsen) und 1-13 (3 Achsen), ergeben sich folgende Werte:
|
|
ZS |
FS |
Summe |
|
2 Achsen |
45 |
39 |
84 |
|
3 Achsen |
91 |
77 |
168 |
|
|
|
|
252 |
|
1 Achse |
15 |
15 |
30 |
|
|
151 |
131 |
282 |
Die beiden Additionswerte sind durch 84 teilbar und verhalten sich somit 1:2. Aus der zyklischen Zahl 252 läßt sich das Produkt 12*21 bilden. Die beiden Zahlen sind durch 3 teilbar und verhalten sich 4:7. Die Zahl 47 erhält man als Teiler, wenn man die ZS u. FS der Zahlen 1-5 für die einachsige Kreisfigur hinzuzieht: 282=6*47.
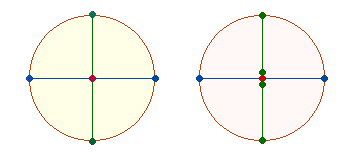
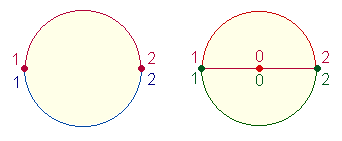
Anmerkung: Die ideelle Vorstellung zweier gleicher Kreise wird inspiriert durch das Zusammenwirken beider Kreisachsen für das Dezimalsystem sowie durch die 8 verschiedenen Buchstaben des Sator-Quadrats mit dem Zahlwert 102, die zu dem Wort PENS||ATOR zusammengefügt werden können und deren Hälften jeweils den Zahlwert 51 für ROTA – Rad haben. Wenn man beide Kreise in zwei Kreishälften teilt, kann man einmal die Kreislinienpunkte mit 1 und 2 bezeichnen und so für die beiden Halbkreisbögen die Umkehrungen 12 und 21 bilden. Auf diese Weise würde dem Prinzip gleicher Hälften, hier 3:3 genüge getan. Wenn man weiterhin eine Durchmesserlinie zieht und den Mittelpunkt mit 0 bezeichnet, lassen sich die Umkehrungen 102 und 201 bilden. Diese doppelte Rechnung ist auch deshalb sinnvoll, weil durch 4*(1+2) die reale zweistellige Zahl 12 entsteht.
|
|
Verbindet man die Elemente der Kreishälften der linken und der rechten Kreisfigur (nun ohne Numerierung), ergibt sich jeweils für die obere und die untere Kreishälfte ohne Mittelteil 1+2=3, für den Mittelteil 2+5=7, zusammen (1+2+1) + (2+5+2) = 3+7+3 = 13. Jede Hälfte mit den Mittelbegrenzungen beträgt (1+2) + (2+5) = 10. Zusammen erhält man 10+10+13 = 33, das ist die Summe der Umkehrungen 12+21.
Das Prinzip ist also, daß die Elemente der ganzen Figur und die Elemente jeder Hälfte addiert werden und so eine neue Gesamtheit erzielt wird.
Bildet man die Faktorenwerte der 4 Zahlen, erhält man als Ergebnis 109, dies ist als 10+9 zu lesen und entspricht der doppelten Zählung der Elemente eines zweiachsigen Achsenkreuzes, einmal 2*5 für jede einzelne Achse und 9 für das gesamte Achsenkreuz.
|
|
ZW |
FW |
|
obere Hälfte |
12 |
7 |
|
|
102 |
22 |
|
untere Hälfte |
21 |
10 |
|
|
201 |
70 |
|
|
336 |
109 |
ANHANG:
1.
Für
die Zusammensetzung der Zahl 10 gibt es verschiedene Modelle, z.B. die Summe
der Zahlen von 1 bis 4 und die 2*5 Radialelemente des Tetraktyssterns. Von
besonderer Bedeutung scheint mir die Addition der 2- und 3-Achsigkeit. Grundgelegt werden die
Zahlen 2 und 3 durch die 2
Linien und 3
Punkte der 5 DM-Elemente. Jede der 5 Achsen schneidet die Kreislinie
in 2 Punkten, damit verdoppelt sich
die Achsenzahl 5 zu 10 Punkten. Auch besteht jede Achse
aus 2 Radiallinien, wodurch zu den 10 Punkten 10 Linien hinzukommen und sich die
Zahl der Elemente auf 20 verdoppelt.
Zu jeder Achse gehört ein
Mittelpunkt, womit die Gesamtzahl von 25 Elementen erreicht ist.
Andererseits besitzt jede der beiden Kreisfiguren nur einen realen Mittelpunkt. Auf diese Weise ergibt
sich wieder eine 2+3-Zählung bzw. eine Doppelzählung
der 20
Symmetrieelemente Elemente, einmal mit 5 und einmal mit 2 Mittelpunkten. Die entsprechende
Rechnung lautet 25+22 = 47. Die Addition 4+7 geht ebenfalls aus der Doppelzählung von 6 Radial- und 5 DM-Elementen hervor: (2L+4P)+(2L+3P).
Faßt man die 20 Symmetrieelemente als eine
Einheit und fügt den Doppelaspekt des Mittelpunktes hinzu, kann man auch einige
relevante 3-stellige Zahlen bilden: 205, 202 und 223 mit ihren Umkehrungen.
2.
Jede
der beiden Achsen entsteht aus einer Anfangsachse. Diese steht bei beiden
Axialfiguren gewissermaßen unsichtbar im Hintergrund. Zählt man sie hinzu,
erhält man die Additionen 1+2 und 1+3 und damit die beiden wichtigsten
trinitarischen Zahlen 3 und 4, die, mit 5 multipliziert, 15+20 = 35 = 7*5 ergeben. Addiert man die Zahl der 5 Achsen einmal
ohne und einmal mit der jeweils unsichtbaren Achse, erhält man 5+7. (2.9.2005)
Erstellt:Dezember 2004