DAS SATOR-QUADRAT
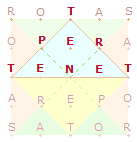
Die zwei frühesten Zeugnisse des SATOR-Quadrats (SQ) wurden 1925 und 1936 in Pompeii
gefunden:
|
|
Letzteres befindet sich, eingeritzt in eine
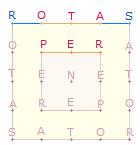
Kannelüre, auf einer Säule der großen Palästra. Im Unterschied zu den meisten
späteren Funden bildet nicht
SATOR, sondern ROTAS die oberste Buchstabenzeile.
Gewöhnlich liest man zeilenweise
von oben nach unten und bemüht sich um den Sinn der 5 Wörter. Kaum jemand denkt
daran, die Lösung in der Natur des Quadrats selbst zu suchen oder sich Gedanken
über das Wesen eines Palindroms zu machen.
In der ersten Hälfte des letzten
Jahrhunderts hat der mathematische Schriftsteller und Rätselspezialist Dr.
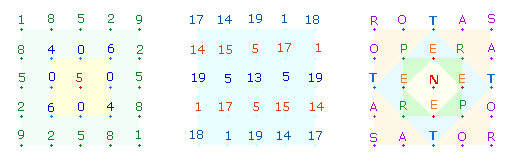
Aloys Christof WILSMANN die 1x1-Tabelle als Modell für das SQ vermutet, wenn
man deren Zehnerstellen sowie die äußeren beiden Tabellenreihen wegläßt (linke
Grafik), so daß die Multiplikationen von 3-7 verlaufen:
|
|
Die Zahlen der untersten
Reihe (von links nach rechts, von unten nach oben) sind mit 3 zu multiplizieren; als erste verläuft die 3-er Reihe demnach in der Folge 9
– 12 – 15 – 18 – 21.
Zwischen den Zahlen des
5x5-Quadrats und den Zahlen des SQ bestehen sinnvolle Beziehungen, die teilweise komplementären
Charakter besitzen.
Wenn das SQ nach einem so grundlegenden
mathematischen Modell gebildet ist, läßt sich vermuten, daß den Buchstaben –
entsprechend ihrem Platz im Alphabet – Zahlenwerte zugrunde liegen. Am Anfang
steht die Vorstellung von mathematischen Ordnungsstrukturen als Analogie und
Abbild göttlicher Wirklichkeit. Der Mensch mit seiner Kultur und Sprache ist
Teil der kosmischen Ordnung. So ist eine Konvergenz von Mathematik, Alphabet
und Sprache innerhalb einer einmaligen politischen und kulturellen Phase der
Menschheitsgeschichte vorstellbar.
Die 25 Buchstaben des SQ sind aus sich
selbst nicht sinnvoll interpretierbar, wie unzähliges Rätselraten beweist.
Ihrem Zustandekommen geht ein mathematischer Reflexionsprozeß über die
Grundlagen des Dezimalsystems aus geometrischen und numerischen Modellen
voraus. Erst am Ende steht gewissermaßen die staunenswerte Umwandlung von
Zahlenstrukturen in Buchstaben und Wörter. Die Auffindung sämtlicher Struktur-
und Bedeutungselemente bleibt eine schwer lösbare Aufgabe.
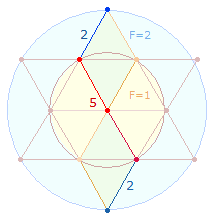
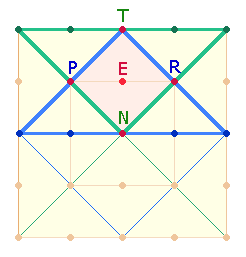
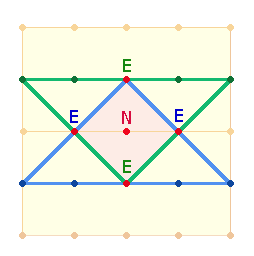
Ein wesentlicher Aspekt des SQ ist die Parallelität seiner zwei konzentrischen
Quadratrahmen zu den zwei konzentrischen Kreisen des Hexagramms:
|
|
|
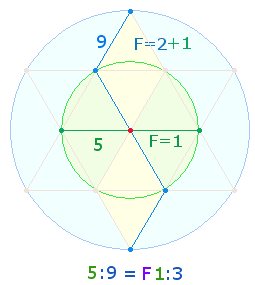
Der Kreisdurchmesser und
eine Quadratseite des inneren Rahmens bestehen aus jeweils 3 Punkten und 2 Linien, zusammen 5 Durchmesserelementen, ein Zickzackdurchmesser des äußeren
Kreises und eine Quadratseite des äußeren Rahmens aus je 5 Punkten und 4
Linien, zusammen 9 Durchmesserelementen. 3 Punkte der inneren Quadratseite sind jedoch auch auf 3 Radialelemente der Kreisachse, bestehend aus 2 Punkten (Mittelpunkt + Kreislinienpunkt) und 1 Radialmaß/Linie, beziehbar, und 5 Punkte der äußeren Quadratseite auf 5 Radialelemente der Zickzacklinie; beides ist zweimal vertreten. Dies zeigt
sich darin, daß die Zahlensumme (ZS)
der 5+3 Buchstaben 69+37 = 106 = 2*53 beträgt, entsprechend der
doppelten Zahl von Radialelementen. Das Verhältnis von 5:3 Radialelementen
enthält eine wesenhafte Analogie zum Flächenverhältnis 3:1 der beiden konzentrischen
Kreise.
Hier ist gleich noch das
System der Faktorenwerte (FW) zu erwähnen. Den ZS 69+37
entsprechen die Faktorensummen (FS)
54+30 = 6*(9:5) =
84. Das FS:ZS-Verhältnis ist demnach 2*(42:53). Auf die Einzelziffern übertragen entsprechen 4:2 Radialmaßen 5:3 Punkte der genannten Zickzacklinie, addiert ergeben sich 9:5 Durchmesserelemente:
|
|
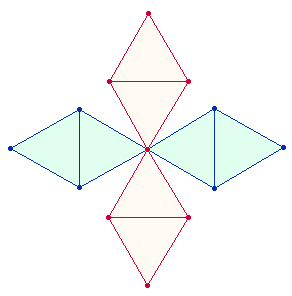
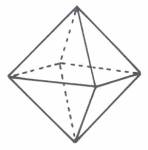
Aus zwei rechtwinklig gekreuzten
Doppelrauten läßt sich ein Oktaeder zusammensetzen, und die Punktestruktur des SQ läßt auch hier eine
Nachahmung zu:
|
|
|
|
|
Auch gegenläufige Dreiecke
lassen sich analog zur doppelten Tetraktys in mehrfacher Weise bilden:
|
|
|
|
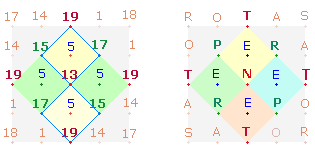
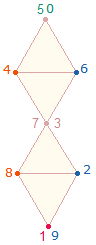
Die genannte 1x1-Tabelle als Modell für das
SQ wird unterstützt durch Zahlenzuordnungen zweier schleifenförmiger
Numerierungen der Doppelraute:
|
|
|
|
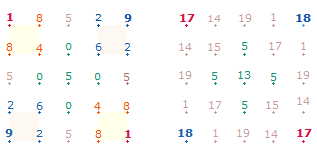
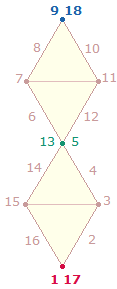
Die Einzelzahlen der 5. und 4. Zeile der 1x1-Tabelle
können von der linken numerierten Doppelraute gegen den Uhrzeigersinn abgelesen
werden (92-81, 26-48) und in den
oberen beiden Zeilen entsprechend im Uhrzeigersinn. Die rechte Doppelraute
zeigt die Zuordnung von 1 und 17 sowie 9
und 18 in den Eckpunkten der Tabelle und des SQ. 5 ist die Komplementärzahl zu 0.
Die mathematische Ordnung des SQ ist so
vollkommen, daß römische Schriftsteller ihrerseits ihren Werken einen
mathematischen Unterbau gaben. Sie waren überzeugt, daß die Objektivität der
Zahl ihren Werken eine überzeitliche Dimension verleihen würde.
Das SQ ist Zeugnis
einer historisch schwer nachweisbaren religiösen Geheimlehre, die in enger
Verbindung mit dem staatlichen VESTA-Kult zu sehen ist. Sie kannte bereits in
vorchristlicher Zeit das Geheimnis des dreieinen Gottes, wie es aus den
Gesetzen des Zahlensystems erkennbar ist. Die normative Kraft des SQ zeigt sich noch in den letzten Jahrzehnten vor Schließung des VESTA-Kultes
395 n. Chr., wie sich aus einer Ehreninschrift für eine Oberverstalin erkennen läßt. Die Verantwortlichen
des Kultes dienten wie eh und je gewissenhaft und hingegeben dem wahren Gott,
waren aber blind und unbelehrbar gegenüber dem Gang der Geschichte, in der sich
das System VESTA in Jesus
Christus bereits
seit einigen Jahrhunderten erfüllt hatte. Sie mußten sich der Macht der neuen
Überzeugungen beugen: Romzentriertes Geschichts- und Heilsdenken hatte seine
Berechtigung verloren.
Das SQ hat heilsgeschichtliche Bedeutung,
d.h., es ist ein UNIKAT, das ein weiteres sinnvolles Buchstabenquadrat
ausschließt. Es ist durch göttliche Weisheit in die lateinische Sprache
hineingeschrieben. Wenn göttliche Weisheit die lateinische Sprache in
untrennbarer Einheit mit dem Bedeutungsystem der Zahlen gestaltete, war es
unausweichlich, die Bedeutung der Wörter und ihrer Zahlenwerte stets neu zu
ergründen.
Wie die alttestamentlichen Propheten, so
weist auch das SQ – mit den Mitteln gematrischer Werte – auf das Kommen des
menschgewordenen Sohnes Gottes IESUS
CHRISTUS voraus. Denn die ZS
182 ist dieselbe von IESUS
CHRISTUS und SATOR OPERA TENET – Der Schöpfer erhält seine Werke:
|
|
ZS |
FS |
sm |
|
IESUS |
70 |
36 |
106 |
|
CHRISTUS |
112 |
76 |
188 |
|
|
182 |
112 |
294 |
Es gibt noch einige weitere
Gemeinsamkeiten: Die ZS+FS (Faktorensumme) 106 von IESUS entspricht der ZS von PER ROTAS (s.o.) – durch Räder, und die FS 76 von CHRISTUS der ZS von TENET AO
– er hält das A und O. Den beiden Summen 112 entsprechen die zweimal vorkommenden Buchstaben AEORT in zweimal NET OPERA SATOR – Es webt die Werke der Schöpfer. Die fünf Buchstaben lassen sich zu ROTAE – Räder, ORTAE – entstanden, geschaffen; abstammend und ORATE – Betet! umstellen. Die zweimal zwei Eckbuchstaben SR haben die ZS 70 von IESUS.
Es ist anzunehmen, daß es Römer gab, die diese
Zusammenhänge erkannten und manche von ihnen auf diese Weise zum Christentum
kamen. Die übrigen freilich waren zu sehr dem politischen und religiösen
Programm römischen Geschichtsdenkens verhaftet, um sich auf ein neues
Verständnis von Staat und Religion umstellen zu können.
Die
Wirkungsgeschichte des SATOR-Quadrats gehört nicht zu meinem
Untersuchungsgegenstand.
Die Forschungs- und Erkenntnismethoden herkömmlicher
Wissenschaft hinsichtlich inhaltlicher Aussage, formaler Grundlagen und
belegbarer Zeugnisse reichen nicht aus, um dem Gegenstand gerecht zu werden.
Gefordert ist eine göttliche Wissenschaft, die das Dezimalsystem als Abbild des
dreieinen Gottes begreift und seine Gesetzmäßigkeiten zu entdecken sucht, so
wie auch Naturwissenschaftler und Techniker nur entdecken und nutzbar machen,
was seit jeher in der Schöpfung vorhanden ist. Göttliche Wissenschaft erfordert
eine Denkweise, die streng rational ist, sich aber übernatürlicher Erleuchtung
öffnet.
Im Sinne herkömmlicher Wissenschaft befaßte sich mit dem SQ am
umfassendsten und gründlichsten der Altphilologe Heinz HOFMANN in Paulys
Realencyclopädie der klassischen Altertumswissenschaft, Supplement 15, 1978,
Sp. 477-565.
Alle
bisherigen Deutungen des SATOR-Quadrats sind mehr oder weniger als geistlose
Raterei zu bezeichnen. Nur mit Bereitschaft zu geistiger Mühe wird auch die
Bereitschaft wachsen, sich mit komplexen Inhalten zu beschäftigen und sich neue
Einsichten anzueigen.
-----------------------------------------------
La VERITÀ STORICA sul QUADRATO del SATOR (Zusammenfassung
wesentlicher Aspekte des SATOR-Quadrats) 2010
Erstellt: 2001
Letzte
Änderung: 2013, 2016, 2020