Die Zahlen 17+16 im Achsenkreuz 5
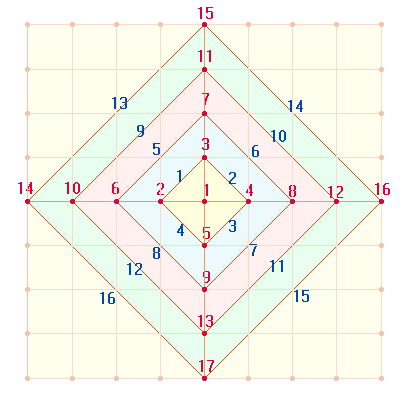
Die Zahlen 1 bis 9 bilden die Grundlage des Dezimalsystems, denn 0 ist nicht zählbar und die Zahl 10 wiederholt bereits die 1. Sie sind als 9 Begrenzungspunkte (P) für 8 Maßeinheiten (L) zu verstehen. Auf diese Weise wird die Zahl 17 zu einer wesentlichen Größe des Dezimalsystems. Legt man durch den Mittelpunkt eine vertikale zweite Achse, übernimmt die 17 die Zahl der Punkte und verdoppelt sich die Zahl der Maßeinheiten auf 16. Wenn man die 4 Winkel spiegelbildlich nach außen projiziert, erhält man ein Quadrat aus 9*9 = 81 Punkten, 64 Quadrateinheiten und (81+64)-1 = 144 Linien. Die Summe der 3 Elemente, (8+9)² = 289 drückt wiederum die Zahl der Achsenelemente aus: 2*(8+9). Die Bedeutung der Quadratzahl von 17 geht auch daraus hervor, daß die FS der trinitarischen Zahl 123 mit ihren Umkehrungen (132, 213, 231, 312, 321) ebenfalls 289 beträgt.
(Die ersten drei
Zahlen 1,2,3 erhält man, wenn man den Achsenmittelpunkt 1 mit der
symmetrischen Zahl der Positionen 16+16 = 32 zusammensetzt: 132 und 321. Die FW dieser beiden Zahlen
ergeben 18+110 = 128 = 4*32. Die Differenz 289-128 = 161
liefert mit 7*23 die Umkehrzahl. Nun bilden 16 und
17 die Mitte der Zahlen 12-21. 12:21 verhält sich 4:7. In den Zahlenreihen 1-21/0-20 spielt die Zahl 32 als Teilerfaktor eine bedeutsame
Rolle.)
Die Zusammengehörigkeit der Zahlen 16 und 17 zeigt sich besonders im Verhältnis der Faktorensummen (FS). Die FS der Zahlen 1-16 beträgt 6*17, für die Zahl 17 erhöht sich die FS auf 7*17, zusammen 13*17 = 221. Die Primzahl 617 ist die Hälfte der ersten vier Zahlen 1234.
Von der Mitte nach außen kann man Punkte und Verbindungslinien der beiden Achsen reihum numerieren. (Die Numerierung der Maßeinheiten folgt hier den eingezeichneten Seiten der konzentrischen Rautenquadrate):
|
|
Die Ordnung dieser Numerierung wird sichtbar, wenn man die Faktorenwerte der Zahlen zusammenzählt. Die folgende Tabelle zeigt zunächst die relevanten Werte von 1 bis 17.
|
Zahl. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
FW |
1 |
2 |
3 |
4 |
5 |
5 |
7 |
6 |
6 |
7 |
11 |
7 |
13 |
9 |
8 |
8 |
17 |
|
ZS |
1 |
3 |
6 |
10 |
15 |
21 |
28 |
36 |
45 |
55 |
66 |
78 |
91 |
105 |
120 |
136 |
153 |
|
FS |
1 |
3 |
6 |
10 |
15 |
20 |
27 |
33 |
39 |
46 |
57 |
64 |
77 |
86 |
94 |
102 |
119 |
|
|
FS |
|
|
|
Gruppe |
Punkte |
Linien |
Summe |
|
1 |
1 |
– |
1 |
|
2 |
14 |
10 |
24 |
|
3 |
24 |
23 |
47 |
|
4 |
38 |
31 |
69 |
|
5 |
42 |
38 |
80 |
|
Summe |
119 |
102 |
221 |
Wenn man unter konzentrischem Gesichtspunkt die Gruppen 1+3+4 und 2+5 zusammenfaßt und nach Punkten und Linien getrennt addiert, erhält man die folgenden proportionalen Ergebnisse:
|
|
Gruppe I: 1+3+4 |
Gruppe II: 2+5 |
||
|
Punkte |
1+24+38 = 63 |
63:54= 9*(7:6) |
14+42=56 |
56:48= 8*(7:6) |
|
Linien |
23+31 = 54 |
10+38=48 |
||
|
Punkte
I:II |
63 : 56 = 7* (9:8) 54 : 48 = 6* (9:8) |
|||
|
Linien I:II |
||||
FW und ZW zusammen
Für die Zahlen 1-16 ist die FS 6*17 = 102, die ZS 8*17 = 136, für die Zahlen 1-17 die FS 7*17
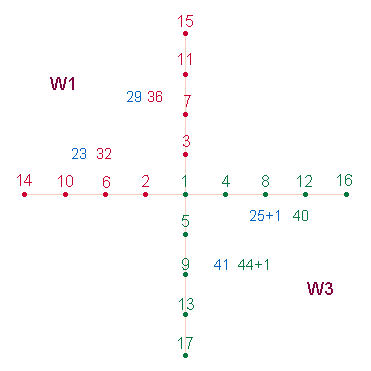
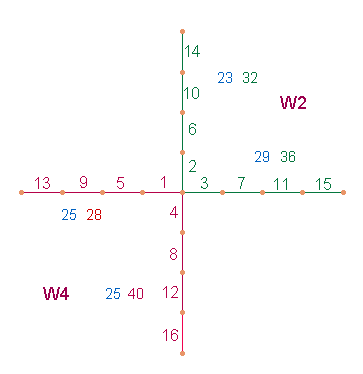
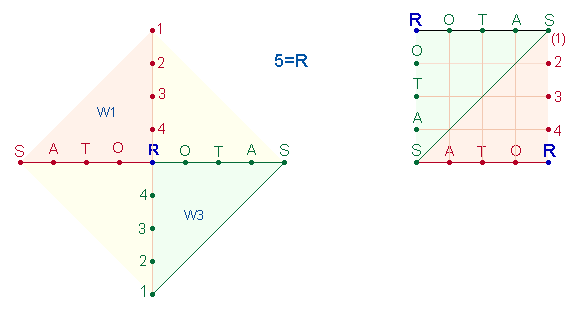
= 119, die ZS 9*17 = 153. Wie ein Vergleich der folgenden zwei
Grafiken zeigt, enthält die horizontale Achse die Zahlen von 1-16 und die
vertikale Achse die Zahlen von 1-17. Jeder Achsenarm enthält ein Reihe von 4
Zahlen. 3 Zahlenreihen sind doppelt vorhanden, die Linienwerte des rechten
Achsenarmes und die Punktewerte des unteren Achsenarmes nur einmal. Wegen der 3
doppelten Zahlenreihen sind die ZW und FW von 16 und 17 nicht nur in der
horizontalen und vertikalen Achse enthalten, sondern auch in der Zusammenfügung
von Winkelseiten. Die FW/ZW von 1-16 lassen sich auf der linken Seite
ermitteln, die FW/ZW von 1-17 auf der rechten Seite. Punktewerte und
Linienwerte stehen sich dabei jeweils diagonal gegenüber.Für jeden Winkel
zählen sowohl FW als auch ZW. Die FW auf beiden Seiten sind blau, die ZW rot
(1-16) und grün (1-17) dargestellt:
|
|
|
|
|
FW |
ZW |
|
|
FW |
ZW |
|
|
||||
|
W1 |
29 |
23 |
36 |
32 |
120 |
W3 |
41 |
26 |
45 |
40 |
152 |
272 |
|
W4 |
25 |
25 |
28 |
40 |
118 |
W2 |
29 |
23 |
36 |
32 |
120 |
238 |
|
|
54 |
48 |
64 |
72 |
|
|
70 |
49 |
81 |
72 |
|
|
|
|
102 |
136 |
238 |
|
119 |
153 |
272 |
510 |
||||
Die Mittelpunktszahl dient häufig als frei verfügbare Ausgleichszahl, die verschiedene mathematische Verhältnisse ermöglicht. Die Zahl 1 wird hier der rechten Seite zugeteilt, und zwar einmal (FW) der horizontalen und einmal (ZW) der vertikalen Achse. Durch diese Verteilung und durch chiastische Anordnung der Werte in der Tabelle ergeben sich für alle benachbarten vertikalen Additionswerte proportionale Verhältnisse, z.B. 54:48 = 6*(9:8), 64:72 = 8*(8:9), 70:49 = 7*(10:7), 81:72 = 9*(9:8)
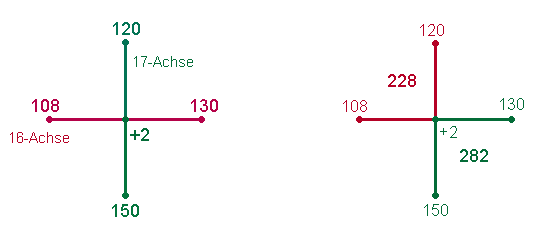
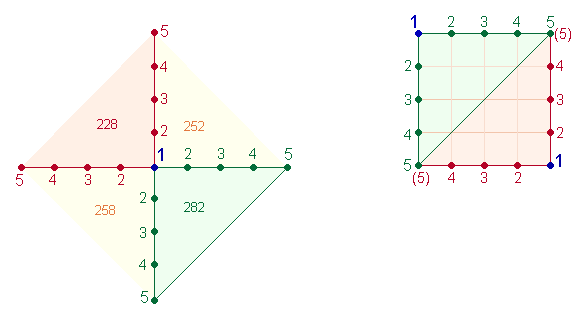
Errechnet man die 4 Werte eines jeden Achsenarms, ergibt sich für die horizontale Achse 108 + 130 = 238 und für die vertikale Achse 120+150+2 = 272.
|
|
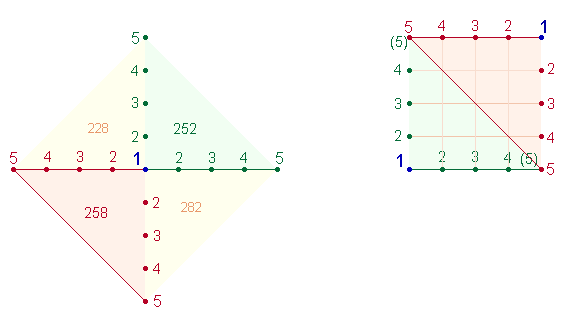
Addiert man alle Werte von Winkel 1 und 3, stehen sich die beiden Umkehrzahlen 108+120 = 228 und 130+150+2 = 282 gegenüber. Das Mittel der beiden Zahlen ist 114 und 141. Sie sind zu lesen als 1+14 und 14+1 und geben viermal die Summe der Zahlen 1-5 wieder, mit denen man, vom Mittelpunkt aus, die 4 Achsenarme besetzen kann. Verschiebt man Winkel 3 diagonal nach oben, bis die Achsenenden zusammentreffen, entsteht ein Quadrat aus 5*5 Punkten und 4*4 Quadrateinheiten. Nach der Verschiebung von Winkel 3 entfällt zweimal die 5, während eine zweite 2 neu hinzutritt. Beginnt man von unten links und liest die Zahlen nach oben, addiert man die die Zahlen 5-2 = 14 und fügt die 1 hinzu. Denselben Vorgang wiederholt man von oben rechts nach links. Die andere Leserichtung beginnt mit der 1 unten rechts nach zwei Richtungen und erhält die umgekehrte Reihenfolge 1+14.
|
|
Die Numerierung 1-5 hat archetypischen Rang, da ein einfaches Achsenkreuz aus 5 Punkten besteht. Den Zahlen 1 und 14 entsprechen im lateinischen Alphabet die Buchstaben A und O. Sie haben im Satorquadrat, das ebenso aus einem 5*5 Punkte Quadrat besteht, eine besondere Bedeutung. Wenn man die Multiplikation 4*14=56 und 1 zu 561 zusammensetzt, erhält man die Summe der 5 Zeilenwerte des Satorquadrates und deren Umkehrungen:
69+52+61+52+69 = 303; 96+25+16+25+96 = 258.
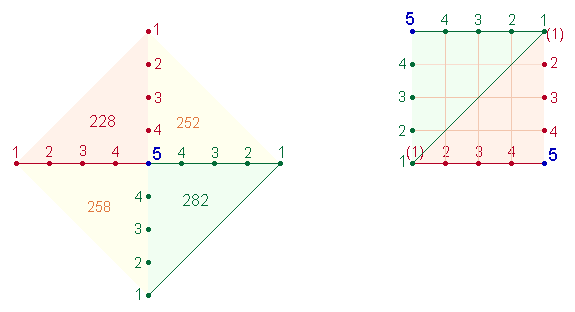
Nun beginnt aber das originale Sator-Quadrat mit dem Wort ROTAS horizontal und vertikal. Wollen wir, daß in der Reihenfolge des A und O Übereinstimmung zwischen dem mathematischen Modell und dem Sator-Quadrat besteht, dann muß man Winkel 4 gegen Winkel 2 verschieben (oder umgekehrt). Das Verhältnis der beiden Zahlen 258:252 ist 6*(43:42).
Wenn wir beide Winkelpaare berücksichtigen wollen, müssen wir in einer zweiten Numerierung die Zahlen 1-5 in Gegenrichtung von außen nach innen auf den Achsenarmen eintragen.
Die beiden Zusammensetzungen der 2. Numerierung lauten 10-5 und 5-10. Im Mittelpunkt steht nun 1+5 = 6, die 32 übrigen Numerierungswerte ergeben 4*(14+10) = 4*24 = 96. Die Gesamtsumme beträgt 6+96 = 102. Diese Zahl entspricht dem Produkt aus dem Mittelwert 3 der beiden komplementären Numerierungen und der Zahl der Einzelwerte 2+32. Eine einzelne Achse hat die Werte 29+25 = 54*2 = 108. Das Verhältnis beider Summen 102:108 ist 6*(17:18).
Soll die linke Quadratseite entsprechend dem Sator-Quadrat mit A=1 beginnen, sind Numerierung und Winkelpaarungen so vorzunehmen:
|
|
|
|
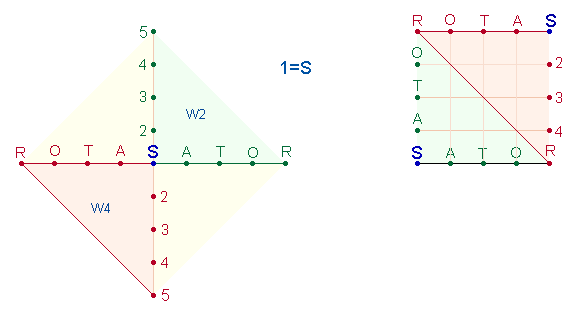
Der Rahmen des Sator-Quadrats im Achsenkreuz 17+16
Wenn ein Quadrat aus einem Achsenkreuz entsteht, kann man den Rahmen des Sator-Quadrats in das entsprechende Achsenkreuz zurückverlegen. Primär ist sicherlich der Begriff SATOR, der spiegelbildlich vom Mittelpunkt nach vier Richtungen zum 5. Punkt fortschreitet. Analog zur komplementären Umkehrnumerierung 5-1 kann man das Wort SATOR auch von außen nach innen schreiben. Dann liest man vom Mittelpunkt aus das Wort ROTAS. Es ist bemerkenswert, daß die Kreisvorstellung des Rades sowohl im Zahlwert der Einzelachse als auch im Gesamtzahlenwert durch eine Quadratzahl sinnfällig wird: Der ZW der Einzelachse ist 11*11 = 121, der ZW des gesamten Achsenkreuzes 15*15 = 225. In der Zahl 15 erscheint die Grundnumerierung eines einfachen Achsenkreuzes von 1-5. Der FW der beiden Achsen ist 2*22 = 44, der FW von 15*15 = 16. Das Verhältnis der beiden Zahlen ist 4*(11+4) = 4*15.Diese FW geben also die Numerierung der vier Achsenarme von 1-5 wieder:
|
|
|
|
Erstellt:November 2004
Letzte Änderung: Februar 2005